


Next: Alapismeretek
Matematika vegyészeknek I.
Vajda Róbert
2002. június 26.
Ennek a rövid dokumentumnak az a célja, hogy összefoglalója legyen a vegyészeknek tartott
matematika gyakorlatok anyagának s így a felkészülésben segítséget nyújtson.
Összefoglaló a feldolgozandó témakörökről:
- Alapismeretek.
- Komplex számok.
- Vektorok.
- Sorozatok.
- Függvényvizsgálat.
- A többváltozós analízis elemei.
- Integrálás
- Alapismeretek.
- Halmazok.
Halmazok megadási módjai. Halmaz műveletek.
A halmazműveletek tulajdonságai. Nevezetes számhalmazok.
 reprezentációja:
A számegyenes. Speciális számhalmazok.
A (binér) reláció fogalma. Nevezetes relációk
reprezentációja:
A számegyenes. Speciális számhalmazok.
A (binér) reláció fogalma. Nevezetes relációk  -n és
-n és  -en.
Relációtulajdonságok.
Azonosságok. Binomiális tétel. A hatványozás azonosságai.
-en.
Relációtulajdonságok.
Azonosságok. Binomiális tétel. A hatványozás azonosságai.
- Nevezetes egyenlőtlenségek.
Háromszögegyenlőtlenség. Számtani-mértani közepek közötti
egyenlőtlenség. Bernoulli-egyenlőtlenség. A Schwarz-egyenlőtlenség.
- A teljes indukció elve.
Az első
 természetes szám összege. Az első
természetes szám összege. Az első
 négyzetszám, köbszám összege. A Bernoulli-egyenlőtlenség bizonyítása.
négyzetszám, köbszám összege. A Bernoulli-egyenlőtlenség bizonyítása.
- Függvények.
A függvény (leképezés) fogalma. Értelmezési tartomány,
értékkészlet. Polinomok, polinomfüggvények. Faktorizáció, polinomosztás.
- Komplex számok.
- Komplex számok.
A számfogalom felépítése. A kompex számok bevezetésének külső és
belső okai. Az imaginárius egység. A kanonikus alak. Reprezentáció:
a komplex számsík. Műveleti szabályok. Komplex számok trigonometrikus
alakja. Szorzás, hatványozás a trigonometrikus alak segítségével.
Négyzetgyökvonás a definíció alapján. Gyökvonás általában.
Az egységgyökök szerepe.
- Vektorok.
- Vektorok.
Műveletek
 -ben. Geometriai jelentés. Vektortér axiómák és egyszerű
következményei. Kitüntetett vektorrendszerek(-halmazok): függetlenség,
generátorrendszer, bázis. A skalárszorzat. Ortogonalitás, norma, metrika.
Az ortonormált bázisok jelentősége. Vektorok hossza, közbezárt szög.
Egyenes egyenlete a síkon. Sík egyenlete térben. A vektoriális
szorzat. A vegyesszorzat. Területszámítás, térfogatszámítás.
-ben. Geometriai jelentés. Vektortér axiómák és egyszerű
következményei. Kitüntetett vektorrendszerek(-halmazok): függetlenség,
generátorrendszer, bázis. A skalárszorzat. Ortogonalitás, norma, metrika.
Az ortonormált bázisok jelentősége. Vektorok hossza, közbezárt szög.
Egyenes egyenlete a síkon. Sík egyenlete térben. A vektoriális
szorzat. A vegyesszorzat. Területszámítás, térfogatszámítás.
- Sorozatok.
- Sorozatok.
Sorozatok mint speciális függvények. Megadási módok. Tulajdonságok:
Korlátosság, monotonitás, torlódási pont. Határérték. Az alapfogalmak
közötti kapcsolatok. Küszöbszámkeresés. Nevezetes határértékek. Divergencia.
Műveleti szabályok. Kiegészítő szabályok.
- Sorozatok határértékének meghatározása I.
Polinomok. A határozatlan kifejezések. Racionális törtkifejezések.
A 'konjugálttal' való szorzás, azonosságok alkalmazása. Mértani sorozatok.
- Sorozatok határértékének meghatározása II.
Összegzések.
 -re visszavezethető feladatok.
Rendőrelv.
-re visszavezethető feladatok.
Rendőrelv.
- Függvényvizsgálat.
- Függvények.
Értelmezési tartomány, zérushelyek, a függvény grafikonja. Inverzfüggvény.
A határérték bevezetése. Folytonosság. Műveleti szabályok. Folytonos
függvények. A Cauchy- és a Heine-definíció ekvivalenciája.
- Függvény határértékének meghatározása.
Összetett függvényekre vonatkozó szabályok. Polinomok. Határozatlan
kifejezések. Racionális törtfüggvények viselkedése a (minusz) végtelenben.
'Konjugáttal' való szorzás.
 , ill.
, ill.
 -re
visszavezethető feladatok. Féloldali határértékek.
-re
visszavezethető feladatok. Féloldali határértékek.
- Deriválás.
A differenciálhányados mint speciális határérték. Geometriai jelentés. Az
érintő egyenesének egyenlete. Az
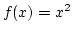 függvény
deriváltfüggvényének meghatározása a definíció alapján. Deriválási
szabályok. Az összetett és az inverzfüggvvény deriváltjára vonatkozó szabály.
Hatványfüggvények, trigonometrikus, exponenciális, logaritmus és
ciklometrikus függvények deriváltja. A szabályok alkalmazása.
függvény
deriváltfüggvényének meghatározása a definíció alapján. Deriválási
szabályok. Az összetett és az inverzfüggvvény deriváltjára vonatkozó szabály.
Hatványfüggvények, trigonometrikus, exponenciális, logaritmus és
ciklometrikus függvények deriváltja. A szabályok alkalmazása.
- A deriválás alkalmazásai.
Határérték meghatározása a derivált segítségével. L'Hospital-szabály.
Szélsőértékfeladatok megoldása. Magasabbrendű deriváltak. A Taylor-
polinom jelentősége.
- Függvénydiszkusszió.
Értelmezési tartomány. Zérushelyek. Az első derivált meghatározása.
Monotonitási tartományok. Lokális szélsőértékek. A második derivált
meghatározása. Konvexitási viszonyok, inflexiós pontok. Határértékek
vizsgálata a kritikus pontokban. Táblázat készítése.
A grafikon vázlata.
- A többváltozós analízis elemei.
- Kétváltozós függvények.
A függvényfogalom kiterjesztése. Ábrázolás. Szintvonalak
Határérték, folytonosság.
- A különböző deriváltak értelmezése.
Parciális derivált. Iránymenti derivált. Totális derivált.
- Alkalmazások.
Érintősík. Lokális szélsőértékek.
- Integrálás
- Határorozatlan integrál.
Primitív függvény. Integrálási szabályok és eljárások.
Parciális integrálás. Integrálás helyettesítéssel.
Racionális törtfüggvények integrálása.
- Határozott integrál
Függvény grafikonja alatti terület. Newton-Leibniz formula.
Függvénygrafikonok által határolt síktartomány területe.
Ívhossz (kerület). Forgástest térfogata.
- Kettős integrál. Vonalintegrál.



Next: Alapismeretek
Róbert Vajda
2003-01-14
 reprezentációja:
A számegyenes. Speciális számhalmazok.
A (binér) reláció fogalma. Nevezetes relációk
reprezentációja:
A számegyenes. Speciális számhalmazok.
A (binér) reláció fogalma. Nevezetes relációk  -n és
-n és  -en.
Relációtulajdonságok.
Azonosságok. Binomiális tétel. A hatványozás azonosságai.
-en.
Relációtulajdonságok.
Azonosságok. Binomiális tétel. A hatványozás azonosságai.
 természetes szám összege. Az első
természetes szám összege. Az első
 négyzetszám, köbszám összege. A Bernoulli-egyenlőtlenség bizonyítása.
négyzetszám, köbszám összege. A Bernoulli-egyenlőtlenség bizonyítása.
 -ben. Geometriai jelentés. Vektortér axiómák és egyszerű
következményei. Kitüntetett vektorrendszerek(-halmazok): függetlenség,
generátorrendszer, bázis. A skalárszorzat. Ortogonalitás, norma, metrika.
Az ortonormált bázisok jelentősége. Vektorok hossza, közbezárt szög.
Egyenes egyenlete a síkon. Sík egyenlete térben. A vektoriális
szorzat. A vegyesszorzat. Területszámítás, térfogatszámítás.
-ben. Geometriai jelentés. Vektortér axiómák és egyszerű
következményei. Kitüntetett vektorrendszerek(-halmazok): függetlenség,
generátorrendszer, bázis. A skalárszorzat. Ortogonalitás, norma, metrika.
Az ortonormált bázisok jelentősége. Vektorok hossza, közbezárt szög.
Egyenes egyenlete a síkon. Sík egyenlete térben. A vektoriális
szorzat. A vegyesszorzat. Területszámítás, térfogatszámítás.
 -re visszavezethető feladatok.
Rendőrelv.
-re visszavezethető feladatok.
Rendőrelv.
 , ill.
, ill.
 -re
visszavezethető feladatok. Féloldali határértékek.
-re
visszavezethető feladatok. Féloldali határértékek.
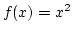 függvény
deriváltfüggvényének meghatározása a definíció alapján. Deriválási
szabályok. Az összetett és az inverzfüggvvény deriváltjára vonatkozó szabály.
Hatványfüggvények, trigonometrikus, exponenciális, logaritmus és
ciklometrikus függvények deriváltja. A szabályok alkalmazása.
függvény
deriváltfüggvényének meghatározása a definíció alapján. Deriválási
szabályok. Az összetett és az inverzfüggvvény deriváltjára vonatkozó szabály.
Hatványfüggvények, trigonometrikus, exponenciális, logaritmus és
ciklometrikus függvények deriváltja. A szabályok alkalmazása.