


Next: 12. Példa
Up: Paricális deriváltak
Previous: 11. Példa
Ha az 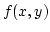 függvény elsőrendű parciális deriváltjai az
függvény elsőrendű parciális deriváltjai az  pont valamely környezetében
folytonosak,
pont valamely környezetében
folytonosak,
 , akkor az
, akkor az 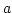 pont egy környezetében
pont egy környezetében
 függvény, hogy
függvény, hogy  , és
, és 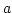 egy környezetében
egy környezetében  , valamint y folytonosan differenciálható és érvényes, hogy
, valamint y folytonosan differenciálható és érvényes, hogy
 .
.
Róbert Vajda
2003-01-14