szeptember 10. Diofantoszi egyenletek
A legnagyobb közös osztó előállítása „lineáris kombinációként”; Euklidész lemmája; a kétismeretlenes lineáris diofantoszi egyenlet megoldhatóságának szükséges és elegendő feltétele, a teljes megoldáshalmaz leírása.
- jegyzet (1.1–1.8)
- euklideszi algoritmus lépésről lépésre
- nyulas játék
- online feladatsorok (lásd a diof, nyul és gombocartur című feladatsorokat)
- Hartmann Miklós matematika gyakorlóoldala (lásd a Legnagyobb közös osztó és a Diofantoszi egyenlet című feladatokat)
Házi feladatok:
- Adja meg a ß117x-36y=63ß diofantoszi egyenlet összes olyan ß(x,y)ß megoldását, amelyre ß0 \leq x,y \leq 20ß teljesül.
- A nyuszifiú a ß0ß-ról indulva, ßa=26ß és ßb=38ß méretű ugrásokkal siet a barátnőjéhez, aki az ß1000ß-es számnál várja. Hogyan juthat el hozzá úgy, hogy folyamatosan közeledjen hozzá (tehát balra nem ugorhat)?
- Valaki a következőket mondta: „A barátnőm 22. születésnapjára 22 szál virágból álló csokrot vettem 2000 forintért. A csokor fréziából, nárciszból és rózsából állt, amelyekből egy szál 50 forintba, 70 forintba, illetve 130 forintba került.” Hány szál virágot tartalmazott az egyes fajtákból a csokor, ha azt is tudjuk, hogy mindegyikből legalább két szál volt, és semelyik kettőből sem volt ugyanannyi?
- Milyen messze van egymástól a ß14x-38y=4ß egyenletű egyenesen két szomszédos rácspont?
- Igaz-e tetszőleges ßa,b,c,dß egész számok esetén, hogy ßa \perp c \implies ab+cd=1ß?
- Adott két szabályos sokszög, az egyiknek ß13ß, a másiknak ß23ß oldala van. Hogyan lehet ennek alapján megszerkeszteni egy szabályos ß299ß-szöget?
szeptember 17. Kongruenciák
A kongruenciareláció fogalma és tulajdonságai; oszthatósági feladatok megoldása kongruenciával; lineáris kongruenciák.
- jegyzet (1.9–1.13)
- nyulas játék
- egy „táblakép” az előadásról
- online feladatsorok (lásd a gyuruk1 című feladatsort)
- Hartmann Miklós matematika gyakorlóoldala (lásd a Lineáris kongruencia című feladatot)
Házi feladatok:
- Mennyi lehet ßmß értéke, ha ß187\equiv5\pmod{m}ß és ß311\equiv3\pmod{m}ß egyszerre teljesül? (Az összes megoldást keressük!).
- Bizonyítsa be kongruenciák segítségével, minél egyszerűbben a héttel való oszthatóságra a következő szabályt: Egy természetes szám akkor és csak akkor osztható ß7ß-tel, ha tízes számrendszerbeli alakjából az utolsó jegyet levágva és a kapott számból a levágott jegy ß2ß-szeresét kivonva, az eredmény osztható ß7ß-tel. Másképp fogalmazva, a ß7 \mid 10a+b \iff 7 \mid a-2bß ekvivalenciát kell igazolni. (Egy példa: ß123452 \rightsquigarrow 12345-4=12341 \rightsquigarrow 1234-2=1232 \rightsquigarrow 123-4=119 \rightsquigarrow 11-18=-7ß, ezért ß123452ß osztható ß7ß-tel.)
- Bizonyítsa be kongruenciák segítségével, minél egyszerűbben, hogy ß27 \mid 2^{5n+1}+5^{n+2}ß minden ßnß természetes szám esetén.
- Oldja meg a ß30x\equiv8\pmod{58}ß lineáris kongruenciát. (A megoldásokat modulo ß58ß kell megadni!)
- Egy nyúl ugrál egy szabályos ß45ß-szög csúcsain a ß0ß-ról indulva. Mekkorákat ugorjon, hogy a ß24ß. ugrással a ß39ß-es csúcsba jusson? (Az összes ß1ß és ß44ß közötti megoldást keressük meg, de persze ne próbálgatással!)
- Oldja meg újra az 1. feladatban szereplő ß117x-36y=63ß diofantoszi egyenletet úgy, hogy átfogalmazza lineáris kongruenciává.
szeptember 24. Maradékosztályok
Maradékosztályok; teljes maradékrendszerek; a maradékosztályok gyűrűje; multiplikatív inverz modulo ßmß; maradékosztálytest; Wilson tétele.
- jegyzet (1.14–1.29)
- gondolatolvasás
- Hartmann Miklós matematika gyakorlóoldala (lásd a Számolás Z_n-ben című feladatot)
Házi feladatok:
- Számítsa ki ß\mathbb{Z}_{18}ß-ban az ß(\overline{5}+\overline{7})^{-1}ß, ß\overline{5}^{-1}+\overline{7}^{-1}ß és ß\overline{5}^{-1}\cdot\overline{7}^{-1}ß elemeket. (Vigyázat: nem mindegyik értelmezett!)
- Számítsa ki ß\mathbb{Z}_{27}ß-ben a ß\overline{2}^{-3}ß és ß\overline{3}^{-2}ß elemeket. (Vigyázat: az egyik nem értelmezett!)
- Mit ad ß19!ß maradékul ß23ß-mal osztva? (Útmutatás: többet ésszel, mint erővel!)
október 1. Az Euler-féle ß\varphiß függvény és az Euler–Fermat-tétel
Az Euler-féle ß\varphiß függvény képlete; redukált maradékrendszerek; az Euler–Fermat-tétel és alkalmazása hatványok maradékainak kiszámítására.
- jegyzet (1.30–1.36)
- hatványozás modulo ßmß
- online tananyag az Euler–Fermat-tételről (a Diszkrét matematika II kurzushoz készült)
- online feladatsorok (lásd az eulerfi1 és eulerfi2 című feladatsorokat)
Házi feladatok:
- Mit ad ß45ß-tel osztva maradékul ß142^{125}ß?
- Mit ad ß98ß-cal osztva maradékul ß109^{81}ß?
- Mit ad ß53ß-mal osztva maradékul ß80^{(111^{50})}ß?
- Milyen számot kell írni ßxß helyére, hogy ß3, 29, 34, 37, 74, xß teljes maradékrendszer legyen modulo ß6ß, és egyúttal redukált maradékrendszer legyen modulo ß7ß?
- Mennyit ad héttel osztva maradékul ß111\cdots 111ß (ß99ß egyes)?
- Hány kilencest kell egymás mellé írni, hogy a kapott ß999\cdots999ß alakú szám osztható legyen ß17ß-tel?
október 8. Kongruenciarendszerek
Lineáris kongruenciarendszer megoldhatóságának szükséges és elegendő feltétele; a teljes megoldáshalmaz leírása; kínai maradéktétel; bijekció ß\mathbb{Z}_{mn}ß és ß\mathbb{Z}_{m} \times \mathbb{Z}_{n}ß között ßm \perp nß esetén.
- jegyzet (1.37–1.43)
- nyulas játék
- illusztráció a ß\xi\colon\mathbb{Z}_{mn}\rightarrow\mathbb{Z}_{m}\times\mathbb{Z}_{n}ß bijekcióhoz
-
a Diszkrét matematika II kurzushoz készült kongruenciarendszeres tananyagok
- interaktív videó kongruenciarendszerekről (Lehet, hogy elnémítva indul, jobboldalt alul lehet bekapcsolni a hangot. Mellette a teljes képrenyőre váltó gomb, az utolsó gombbal pedig be lehet zárni a bal oldali tartalomjegyzéket.)
- a videóban használt prezentáció (pdf)
- a videóban használt nyulas játék
- Hartmann Miklós matematika gyakorlóoldala (lásd a Kongruenciarendszer és Kínai maradéktétel című feladatokat)
Házi feladatok:
- Állítsa be ebben az illusztrációban a sorok hosszát ß100ß-ra, a minta hosszát pedig ß102ß-re. Lesz-e balról az ötödik oszlopban (amelyikben ß4ß-es áll legfelül) olyan szám, ami pont olyan színű, mint a ß8ß-as? És olyan, ami pont olyan színű, mint a ß9ß-es? Ha igen, akkor melyik ez a szám? Ha nem, akkor miért nincs? (A megoldást természetesen ki kell számolni, nem pedig az ábráról leolvasni!)
- Oldja meg az alábbi lineáris kongruenciarendszert. ßß \left. \begin{array} [c]{r}% 3x\equiv5~\left( \operatorname{mod}10\right) \\ 3x\equiv17~\left( \operatorname{mod}8\right) \\ 14x\equiv10~\left( \operatorname{mod}6\right) \end{array} \right\} ßß
- A kínai maradéktétel segítségével oldja meg az alábbi paraméteres lineáris kongruenciarendszert. ßß \left. \begin{array} [c]{c}% x\equiv a~\left( \operatorname{mod}3\right) \\ x\equiv b~\left( \operatorname{mod}4\right) \\ x\equiv c~\left( \operatorname{mod}5\right) \end{array} \right\} ßß
- A 3d osztály kirándulni ment. Ötfős szobákban szállásolták el őket, így négy gyerek kénytelen volt Marcsi nénivel egy szobában aludni. Éjszaka Bence olyan rosszul viselkedett, hogy Marcsi néni felhívta a szüleit, akik már hajnalban hazavitték. Így a reggelinél szépen elfértek a gyerekek a hétszemélyes asztaloknál (Marcsi néni külön asztalnál ült). Panka gyomorrontást kapott a reggelitől, ezért délelőtt őt is hazavitték. Ebédnél az étteremben minden asztalnál kilenc gyerek ült (Marcsi néni külön asztalnál). Hányan járnak a 3d osztályba?
- Milyen szabály szerint vannak beírva a számok az alábbi ß7 \times 5ß-ös táblázatba? Adja meg képlettel az ßiß-edik sor ßjß-edik oszlopában álló számot (ßiß és ßjß függvényében). A sorokat és az oszlopokat nullától kezdve számozzuk, ahogy az ábra mutatja.
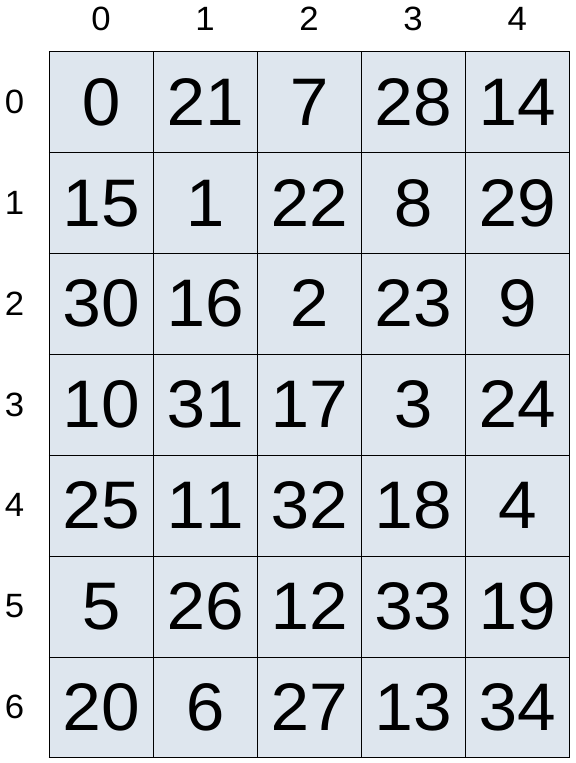
- Jancsi kölcsönkérte Juliska algebra és számelmélet jegyzetét, de véletlenül leöntötte sörrel, ezért az alábbi kongruenciarendszerben és a megoldásában néhány szám olvashatatlan lett: ßß \left. \begin{array} [c]{r}% 14x\equiv\ldots~\left( \operatorname{mod}10\right) \\ 19x\equiv\ldots~\left( \operatorname{mod}15\right) \\ \ldots x\equiv\ldots~\left( \operatorname{mod}18\right) \end{array} \right\} \qquad\text{Mo.: } \underline{\underline{x\equiv\ldots~(\operatorname{mod}30)}}. ßß Jancsi úgy gondolja, hogy a megoldás biztosan hibás, mert nem stimmel a modulus. Igaza van-e Jancsinak? Ha igen, akkor bizonyítsa be, hogy bármilyen számok is vannak az elmosódott helyeken, a megoldás semmiképpen nem lehet jó. Ha nincs igaza, akkor adjon meg olyan számokat, amiket az elmosódott helyekre írva jó lesz a megoldás.
október 15. Számelméleti függvények
A számelméleti függény fogalma; gyenge multiplikativitás; nevezetes számelméleti függvények (ß\varphi, \tau, \sigmaß) gyenge multiplikativitása és képlete.
október 22. Diofantoszi egyenlet polinomgyűrűben + első zh
Az ßfu+gv=hß alakú egyenletek megoldása test feletti polinomgyűrűben.
- jegyzet (3.1–3.16)
- diofantoszi egyenlet polinomokra (két kidolgozott feladat)
- Hartmann Miklós matematika gyakorlóoldala (lásd a Polinomok: maradékos osztás, Polinomok: lnko és Polinomok: diofantoszi egyenlet című feladatokat)
-
Diszkrét matematika 3 videók polinomokról
- alapvető definíciók (elmélet)
- oszthatóság (elmélet)
- legnagyobb közös osztó (elmélet)
- polinomok legnagyobb közös osztója (feladatmegoldás)
- diofantoszi egyenlet polinomgyűrűben (feladatmegoldás)
- polinomok közös gyökei (feladatmegoldás)
Házi feladatok:
- Számítsa ki az ßfß és ßgß polinomok legnagyobb közös osztóját, és adja meg az ßfu+gv=\operatorname{lnko}(f,g)ß egyenlet egy megoldását az ß\mathbb{R}[x]ß polinomgyűrűben: ßßf=x^4+2x^3-x^2-4x-2, \qquad g=x^4+x^3-x^2-2x-2.ßß
- Számítsa ki az ßfß és ßgß polinomok legnagyobb közös osztóját, és adja meg az ßfu+gv=\operatorname{lnko}(f,g)ß egyenlet egy megoldását az ß\mathbb{R}[x]ß polinomgyűrűben: ßßf=x^3-7, \qquad g=2-x.ßß
- Adja meg az ßfu+gv=\overline{1}ß egyenlet egy megoldását a ß\mathbb{Z}_5[x]ß polinomgyűrűben: ßßf=x^3+x^2+\overline{2}, \qquad g=\overline{2}x^2+x+\overline{3}.ßß
- Ábrázolja a 12. egységgyököket a komplex számsíkon, és mindegyikhez írja oda, hogy ő hányadik primitív egységgyök.
október 29. Tökéletes számok; az Euler-féle ß\varphiß függvény összegzési függvénye.
Euler tétele a páros tökéletes számokról; Mersenne- és Fermat-prímek; az Euler-féle ß\varphiß függvény és a komplex egységgyökök; az Euler-féle ß\varphiß függvény összegzési függvénye.
- jegyzet (2.10–2.18)
- Mersenne- és Fermat-prímek
- Great Internet Mersenne Prime Search
- Prime factors ßk \cdot 2^n + 1ß of Fermat numbers ßF_mß and complete factoring status
- Konvolúció, Möbius-féle inverziós formula (1–12. old.)
Házi feladatok:
- Mennyi ß7!ß osztóinak száma és osztóinak összege?
- Melyik az a legkisebb természetes szám, amelynek pontosan ß25ß osztója van?
- Határozza meg az összes olyan ßnß természetes számot, amelyekre ß\sigma(n)=114ß.
- Dávid kapott egy zacskó gumicukrot, amiben 30 gumimaci volt. Ezeket háromféleképpen tudta téglalap alakban elrendezni az asztalon:
Ha legközelebb egy sokkal nagyobb zacskóval kap, amelyben googol db gumimaci van, azokat hányféleképpen fogja tudni elrendezni? (googolß=10^{100}ß)

- Dávid unja már a téglalapokat; most másképp rendezte el a gumicukrokat:
Ha tényleg megkapja a googol db gumimacit, azokat hányféleképpen fogja tudni így elrendezni?

november 5. Összegzési és megfordítási függvény; polinomok maradékosztály-gyűrűi; irreducibilis polinomok véges testek felett.
Összegzési és megfordítási függvény; konvolúció; Möbius-féle ß\muß függvény; Möbius-féle inverziós formula; kongruencia és maradékosztályok test feletti polinomokra; a ßT[x]/(m)ß maradékosztály-gyűrű; irreducibilitás és gyökök kapcsolata; irreducibilis felbontás ß\mathbb{Z}_pß felett.
- jegyzet (2.19–3.34)
- Konvolúció, Möbius-féle inverziós formula (13–21. old.)
- az Algebra és számelmélet (BSc) tantárgyhoz készített prezentáció irreducibilis polinomokról (9–16. old.)
Házi feladatok:
A 36. feladat még él!
- Legyen ßfß az ßF(n)=n^2ß számelméleti függvény megfordítási függvénye. Határozza meg ßf(12)ß értékét.
- Bontsa irreducibilis polinomok szorzatára az ßx^5 + x^4 + \overline{2}x^3 + \overline{2}x + \overline{1} \in \mathbb{Z}_3[x]ß polinomot.
- Bontsa irreducibilis polinomok szorzatára az ßx^5 + \overline{6}x^4 + x^3 + \overline{6}x^2 + \overline{2}x + \overline{5} \in \mathbb{Z}_7[x]ß polinomot.
- Határozza meg az összes legfeljebb harmadfokú irreducibilis polinomot ß\mathbb{Z}_2ß felett.
- Irreducibilis-e az ßx^4+x+\overline{1}ß polinom ß\mathbb{Z}_2ß felett? (Fel lehet használni az előző feladat eredményét.)
november 12. Relációk: ekvivalenciák és részbenrendezések.
Ekvivalenciarelációk és osztályozások; leképezés magja; részbenrendezett halmazok; minimális, maximális, legkisebb és legnagyobb elemek.
- jegyzet (4.1–4.28)
- gyakorló feladatok
- Hartmann Miklós matematika gyakorlóoldala (lásd az Osztályozások című feladatot)
- Ekvivalenciarelációk a számfogalom felépítésében
- Diszkrét matematika 1 tananyagok relációkról
november 19. Polinomgyűrű maradékosztályteste; irreducibilis polinomok a racionális számtest felett; szimmetrikus polinomok.
Polinomgyűrű maradékosztályteste; véges testek; egyszerű algebrai bővítés; bonyolultabb nevezők gyöktelenítése; Rolle(?) tétele; egész együtthatós polinom ß\mathbb{Q}ß és ß\mathbb{Z}ß feletti felbontásainak kapcsolata; Kronecker módszere; Schönemann–Eisenstein-tétel; racionális törtek felbontása elemi törtek összegére; Viéte-formulák és szimmetrikus polinomok; a szimmetrikus polinomok alaptétele; algebrai és transzcendens számok; gyökmennyiségek.
- jegyzet (3.35–3.79)
- Irreducibilis polinomok, elemi törtekre bontás (9–40. old.)
- Szimmetrikus polinomok, algebrai és transzcendens számok
- online feladatsorok (lásd az irred című feladatsort)
Házi feladatok:
- Határozza meg az ß5x^8 - 5x^7 + 4x^2 - 2x - 2ß polinom irreducibilis felbontását ß\mathbb{Q}ß felett.
- Határozza meg az ßx^6 + 125ß polinom irreducibilis felbontását ß\mathbb{Q}ß felett. (Útmutatás: Itt nem segít se a Rolle(?)-tétel se a Schönemann–Eisenstein-tétel, de a ß\mathbb{C}ß feletti felbontásból meg lehet határozni az ß\mathbb{R}ß felettit, majd abból a ß\mathbb{Q}ß felettit.)
- Adjon meg egy olyan ßnß pozitív egész számot, amelyre a ß20x^{2020} + 2020x + nß polinom irreducibilis ß\mathbb{Q}ß felett, és egy olyat is, amelyre nem irreducibilis.
november 26. Permutációk.
A permutáció fogalma; permutációk szorzása és hatványozása; idegen permutációk felcserélhetősége; felbontás idegen ciklusok szorzatára; felbontás transzpozíciók szorzatára; páros és páratlan permutációk; a szimmetrikus és az alternáló csoport.
- jegyzet (5.1–5.16)
- gyakorló feladatok
- Hartmann Miklós matematika gyakorlóoldala (lásd a Permutációk: ciklusfelbontás és Permutációk: szorzás című feladatokat)
- Diszkrét matematika 3 tananyagok permutációkról
december 3. Nevezetes számelméleti problémák: hatványösszegek és prímszámok
A primitív pitagoraszi számhármasok leírása; nagy Fermat-tétel; Fermat-féle kétnégyzetszám-tétel; Lagrange-féle négynégyzetszám-tétel; Waring problémakör; végtelen sok (ß4k-1ß alakú) prím létezése; Dirichlet tétele a számtani sorozatokban előforduló prímekről; Csebisev tétele; nagy és kis hézagok a prímek között; felső becslés az ßnß-edik prímszámra; prímszámtétel; a prímharmonnikus sor divergenciája.
- jegyzet (6.1–6.28)
- Nevezetes számelméleti problémák
- Distribution of the Last Digit of the Primes (Wolfram Demonstrations)
- a prímszámok eloszlása (cdf)
- Fazekas Róbert: A Waring-sejtés bizonyítása (szakdolgozat, SZTE, 2015)
- Körmendi Kristóf: A Dirichlet-tétel (szakdolgozat, SZTE, 2009)
- Szabó Lilla: A prímszámtétel bizonyításának története (szakdolgozat, SZTE, 2014)
- komplex gyökvonás (játék)