Valós függvények, határérték, folytonosság

Definíciók

2.1

Inverz függvény

2.2

Korlátosság,monotonitás

2.3

Konvex és konkáv függvény

2.4

Lokális szélsôérték és inflexiós pont

2.5

Határérték (mínusz) végtelenben ( $\lim_{x\to -\infty} f(x),\, \lim_{x\to \infty} f(x)$)

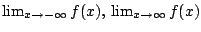2.6

(Féloldali) határérték véges pontban ( $\lim_{x\to x_0} f(x),\, \lim_{x\to x_0^-} f(x),\, \lim_{x\to x_0^+} f(x)$)

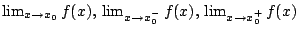2.7

Folytonosság (Cauchy és Heine féle def. is!)

2.8

Egyenletes folytonosság

Tételek

2.1

Határértékre és folytonosságra vonatkozó mûveleti szabályok

2.2

$\lim_{x\to 0}{\sin x\over x},\, \lim_{x\to \infty} (1+1/x)^x$

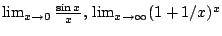
2.3

Elemi függvények folytonossága

2.4

Korlátos zárt intervallumon folytonos függvény korlátos

2.5

Korlátos zárt intervallumon folytonos függvény szélsôértékei

2.6

Korlátos zárt intervallumon folytonos függvény egyeneletesen folytonos

Bizonyítások

2.1

Korlátos zárt intervallumon folytonos függvény korlátos

2.2

Korlátos zárt intervallumon folytonos függvény egyeneletesen folytonos