


Next: Példa
Up: Határozott integrál
Previous: Példa
Egy test gyorsulása a '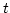 '-edik másodpercben:
'-edik másodpercben:
![$a(t)=3\sin(2t) [{m\over{s^2}}]$](img579.png) , továbbá tudjuk,
hogy
, továbbá tudjuk,
hogy 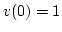 és
és
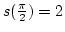 . Mennyi utat tesz meg '
. Mennyi utat tesz meg '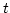 ' másodperc elteltével? Mennyi az átlagsebessége
a
' másodperc elteltével? Mennyi az átlagsebessége
a 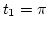 és a
és a 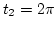 közötti időintervallumban?
közötti időintervallumban?
Megoldás:
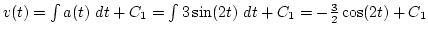 , és mivel
, és mivel 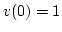 , így
, így
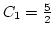 .
.
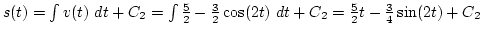 , és mivel
, és mivel
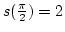 , így
, így
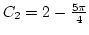 .
.
Róbert Vajda
2003-01-14
![]() , és mivel
, és mivel ![]() , így
, így
![]() .
.
![]() , és mivel
, és mivel
![]() , így
, így
![]() .
.