


Next: Példa
Up: Határozott integrál
Previous: Helyettesítés határozott integrál esetén
Határozzuk meg az egység sugarú (negyed-)kör területét.
Megoldás: Az origó középpontú 1 sugarú kör egyenlete : 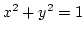 , ezért az első síknegyedet választva
az explicit függvénykapcsolatot az
, ezért az első síknegyedet választva
az explicit függvénykapcsolatot az
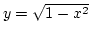 képlet írja le. A meghatározandó integrál tehát:
képlet írja le. A meghatározandó integrál tehát:
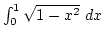 . Alkalmazzuk a
. Alkalmazzuk a 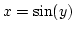 helyettesítést.
helyettesítést.
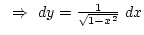
![$\int_0^1 \sqrt{1-x^2} dx=\int_0^{\pi\over2} 1-\sin^2(y) dy=\int_0^{\pi\over2} \...
...\cos(2y) dy={1\over2}\left[y+{\sin(2y)\over2}\right]_0^{\pi\over2}={\pi\over4}$](img574.png) .
.
Ezért az egészkörnek a területe 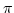 , és a hasonlóság miatt az R sugarú kör területe
, és a hasonlóság miatt az R sugarú kör területe
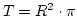 .
.
2. Megoldás. Ha ismerjük a polárkoordinátákra vonatkozó területképletetet, akkor gyorsabban
célhoz érünk:
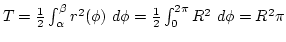 .
.
Róbert Vajda
2003-01-14
![$\int_0^1 \sqrt{1-x^2} dx=\int_0^{\pi\over2} 1-\sin^2(y) dy=\int_0^{\pi\over2} \...
...\cos(2y) dy={1\over2}\left[y+{\sin(2y)\over2}\right]_0^{\pi\over2}={\pi\over4}$](img574.png) .
.
![$\int_0^1 \sqrt{1-x^2} dx=\int_0^{\pi\over2} 1-\sin^2(y) dy=\int_0^{\pi\over2} \...
...\cos(2y) dy={1\over2}\left[y+{\sin(2y)\over2}\right]_0^{\pi\over2}={\pi\over4}$](img574.png) .
.
![]() , és a hasonlóság miatt az R sugarú kör területe
, és a hasonlóság miatt az R sugarú kör területe
![]() .
.
![]() .
.