Páros gráfok
1. feladat. Térjünk vissza a korábban és már azelőtt is emlegetett 6 fős társasághoz:
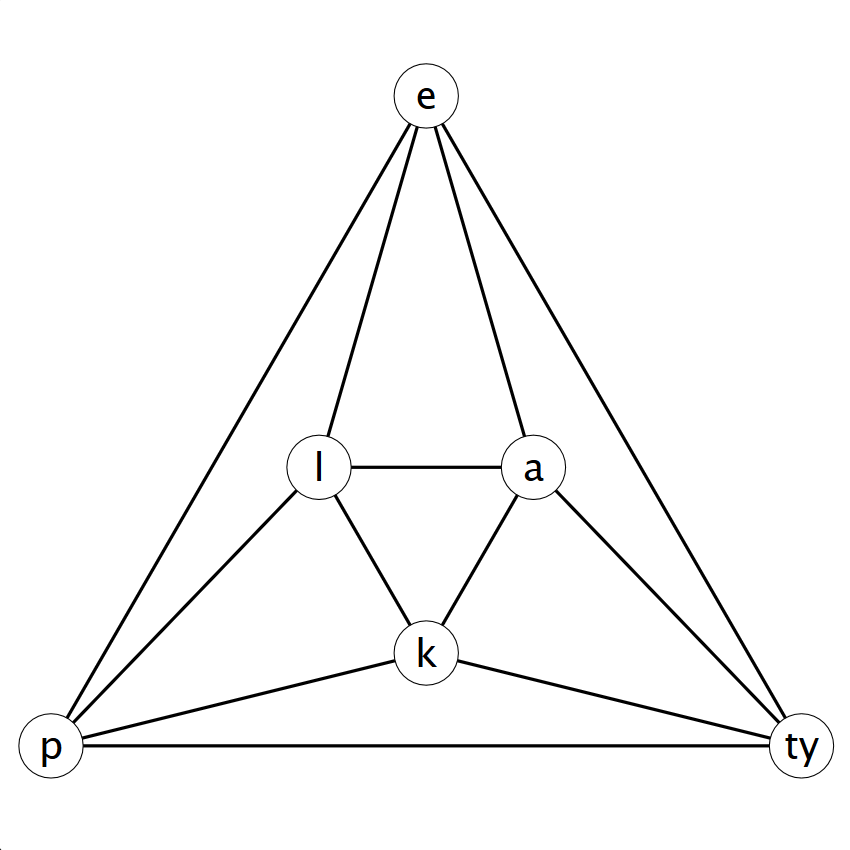
Lehetséges-e, hogy mindenkinek csak ellenkező nemű ismerőse van?
Gráfon továbbra is mindig véges irányítatlan gráfot értünk, amelyben nincsenek se hurokélek se többszörös élek. Mielőtt megnézed a feladatok megoldásait, gondolkozz, és próbáld önállóan megoldani őket, majd vesd össze a megoldást a sajátoddal!
1. feladat. Térjünk vissza a korábban és már azelőtt is emlegetett 6 fős társasághoz:

Lehetséges-e, hogy mindenkinek csak ellenkező nemű ismerőse van?
Megoldás: Nem lehetséges; pl. az l-a-k „szerelmi háromszögben” biztosan van két azonos nemű ember.
2. feladat. És ebben a társaságban lehetséges, hogy mindenkinek csak ellenkező nemű ismerőse van?
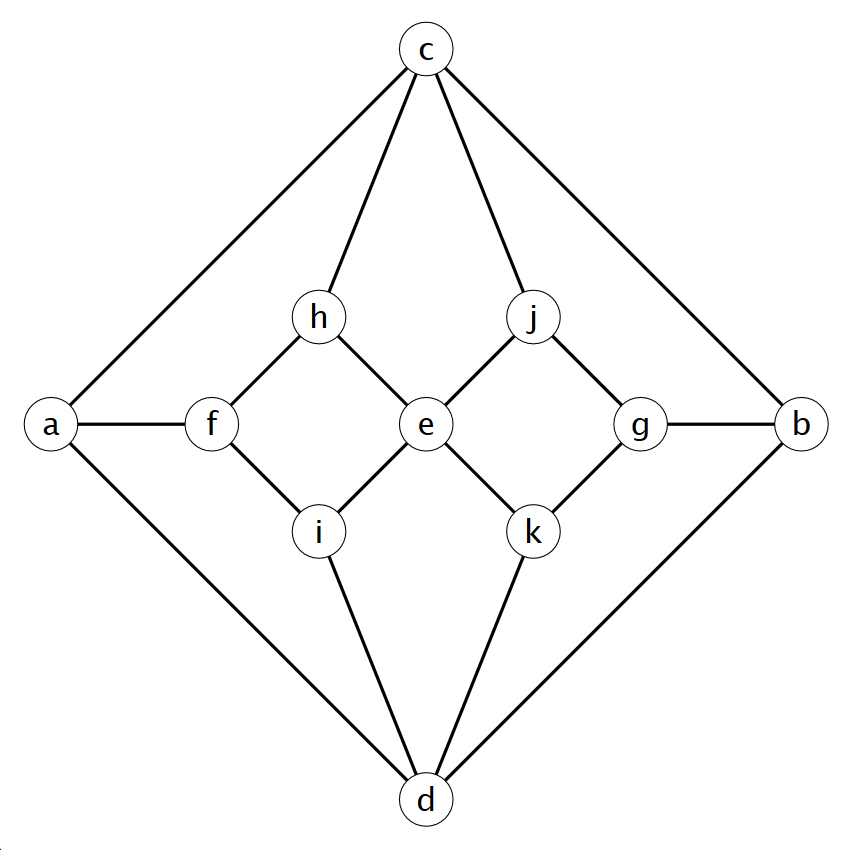
Megoldás: Igen, például így (rózsaszín jelzi a nőket, és kék a férfiakat, vagy fordítva):
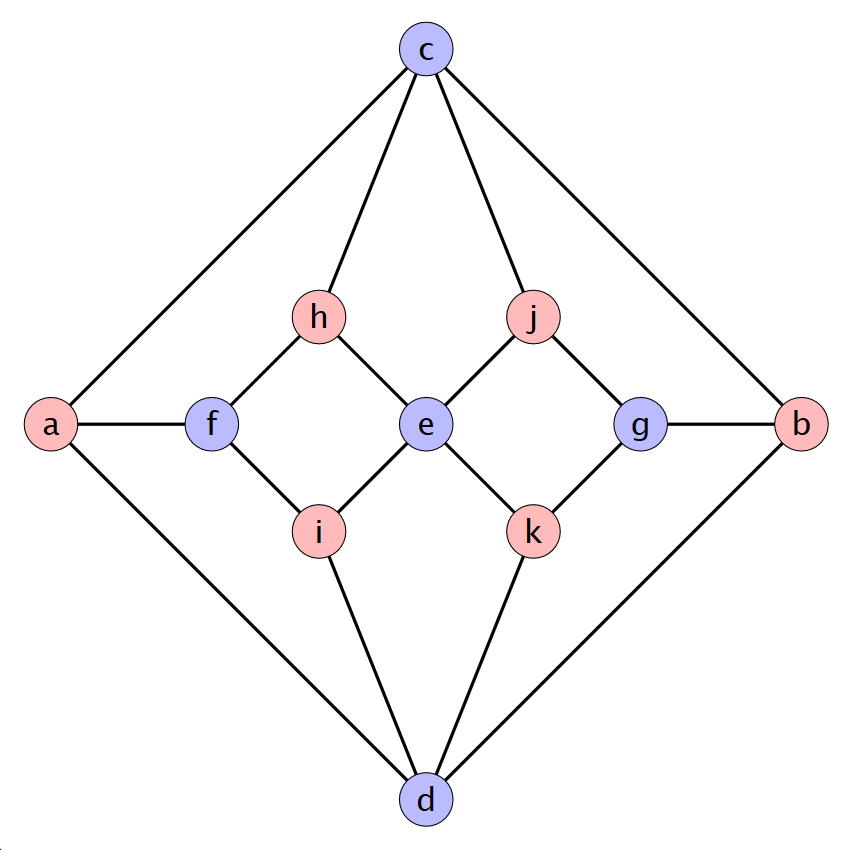
Vesd össze ezt az ábrát a saját megoldásoddal. Neked is ugyanez a férfi-nő felosztás jött ki (a két nem esetleges felcserélésétől eltekintve)?
Korábban azt állítottuk, hogy ebben a gráfban nincs Hamilton-kör (Hamilton-utat már valószínűleg találtál benne). Hogyan tudnád a fentiek fényében ezt kimerítő esetvizsgálatok nélkül bebizonyítani?
Ha lenne Hamilton-kör, akkor tudna ez a társaság körtáncot járni úgy, hogy mindenki két ismerősének a kezét fogja. Ez pedig nem lehetséges, mert akkor a körben felváltva lennének a nők és a férfiak, de 6 nő van és 5 férfi.
Ha egy gráf csúcsait fel lehet osztani két csoportra (nők és férfiak) úgy, hogy minden él „keresztbe ” menjen a két csoport között, akkor a gráfot páros gráfnak nevezzük. (Angolul bipartite graph az elnevezés, ami szó szerint „két részből álló gráfot” jelent. Ez egy kissé körülményes elnevezés, de jobban fedi a fogalom tartalmát, mint a „páros gráf”. Jegyezzük meg: a nem páros gráfra nem mondjuk azt, hogy páratlan!) Ahogy a fenti ábra mutatja, egy gráf akkor és csak akkor páros, ha a csúcsait ki lehet színezni két színnel úgy, hogy azonos színű csúcsok között nem fut él. A páros gráfokat szokás úgy lerajzolni, hogy az egyik osztályba tartozó csúcsokat fölülre, a másik osztályba tartozókat alulra rajzolják:
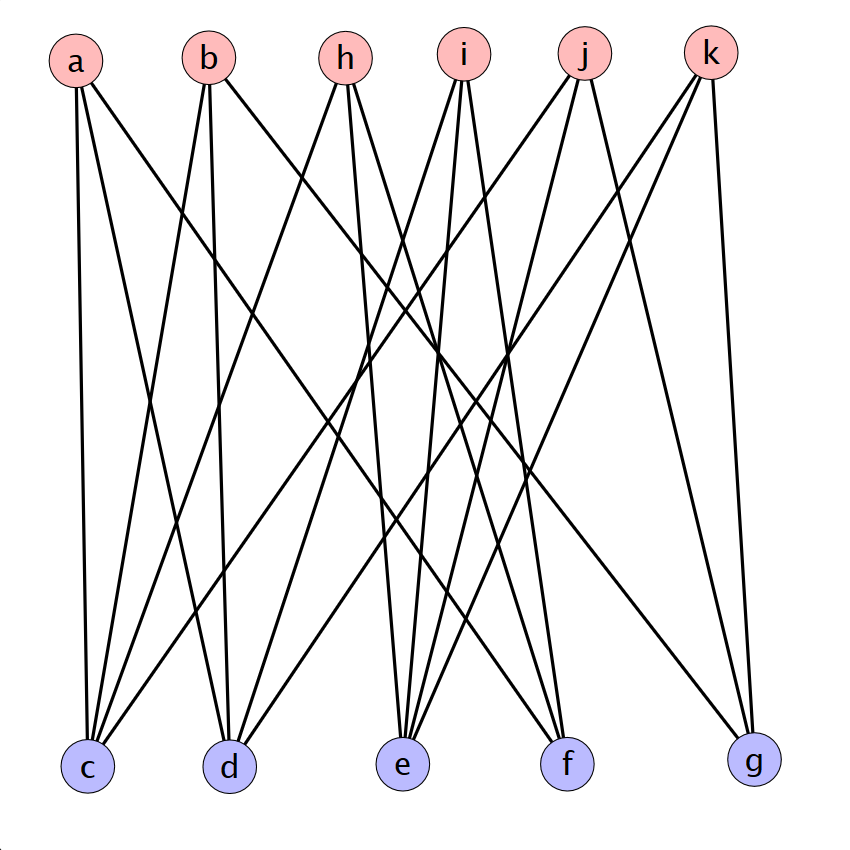
Nem állítom, hogy ettől áttekinthetőbb lett a gráf, de az jól látszik, hogy valóban páros.
Az előző két példában látottak alapján leszűrhetjük azt a tanulságot, hogy ha egy gráfban van páratlan hosszúságú kör, akkor az nem lehet páros gráf. (Az 1. feladatbeli háromszög egy páratlan hosszúságú kör, a 2. feladatban pedig igazából nem volt fontos a „Hamiltonság”; abban a gráfban semmilyen páratlan hosszúságú kör nem létezik.) Ennek a megfordítása is igaz: ha a gráf nem páros, akkor szükségképpen tartalmaz páratlan hosszú kört. A bizonyítás nem túl nehéz; lásd az előadás anyagában; a 2861–2878. oldalakon. Összefoglalva:
Tehát könnyű bizonyítékot szolgáltatni arra, hogy egy gráf (nem) páros: ha páros, akkor megadjuk egy színezését két színnel (vagy pedig egy „alsó-felső” lerajzolását); ha nem páros, akkor megadunk benne egy páratlan hosszú kört.
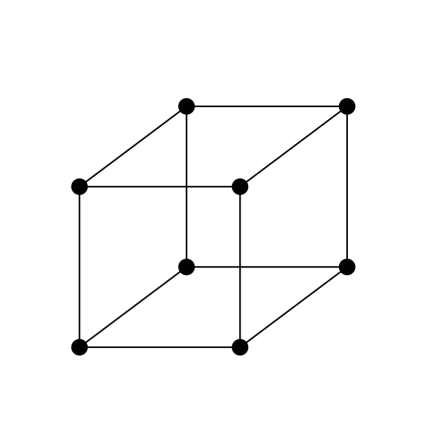
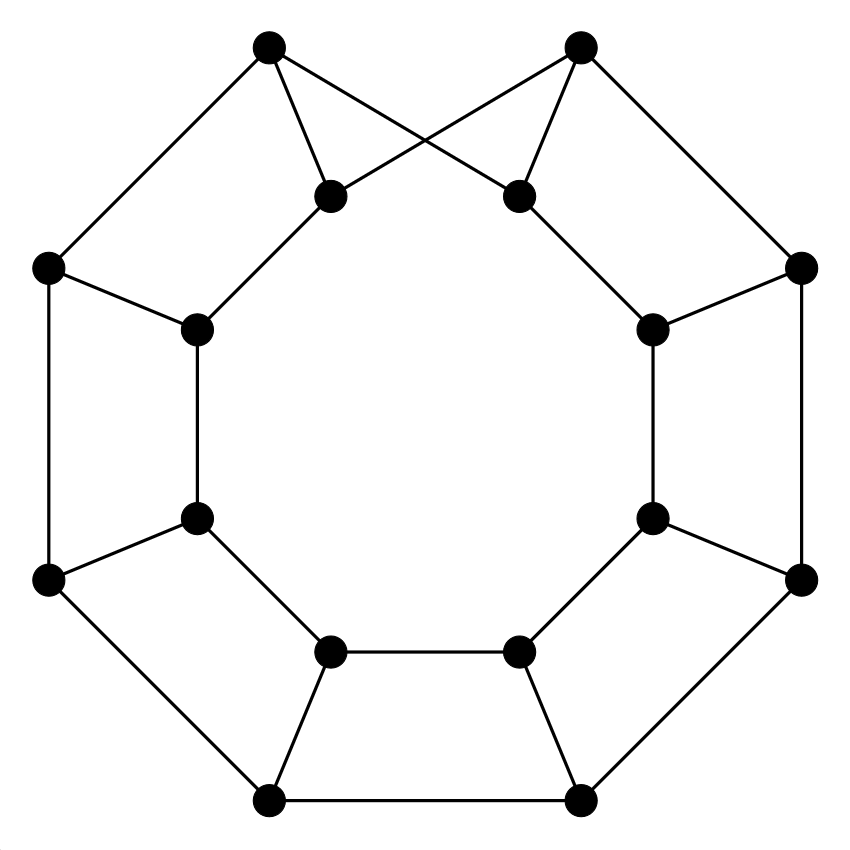
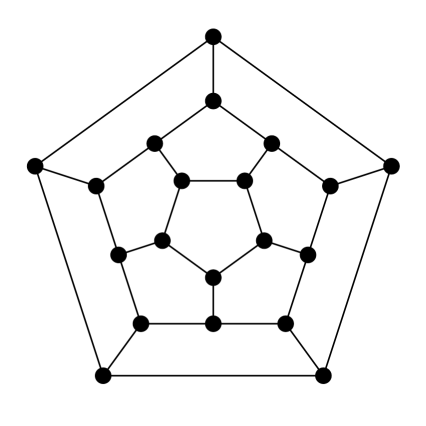
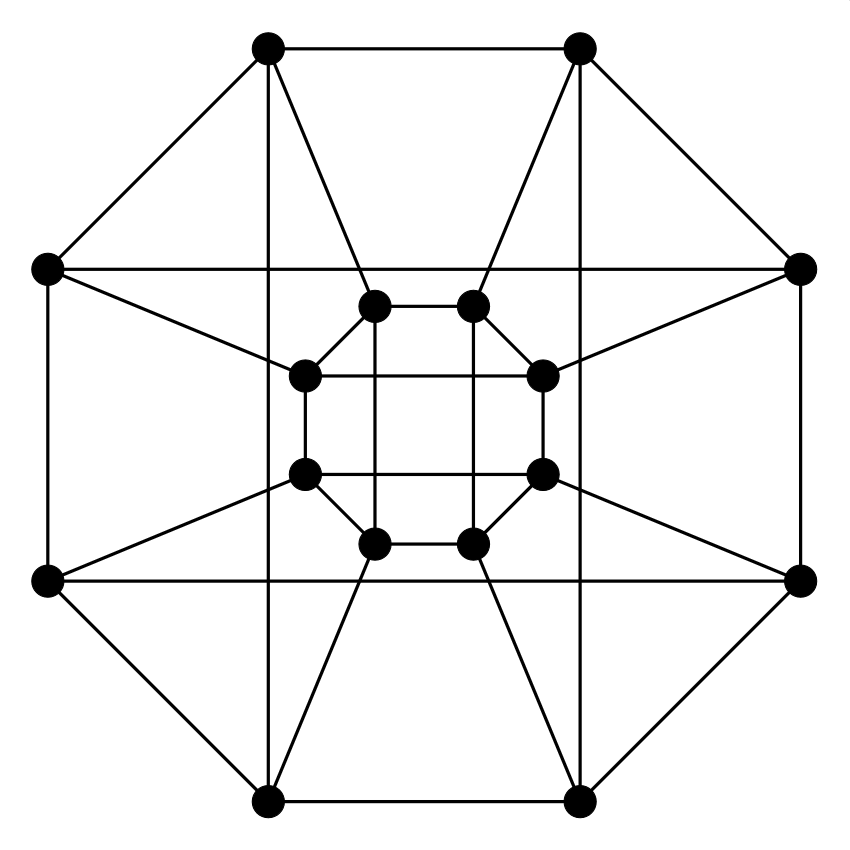
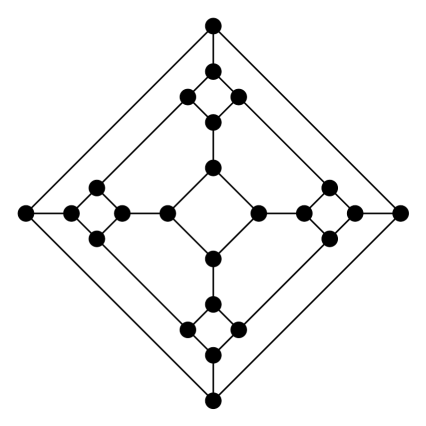
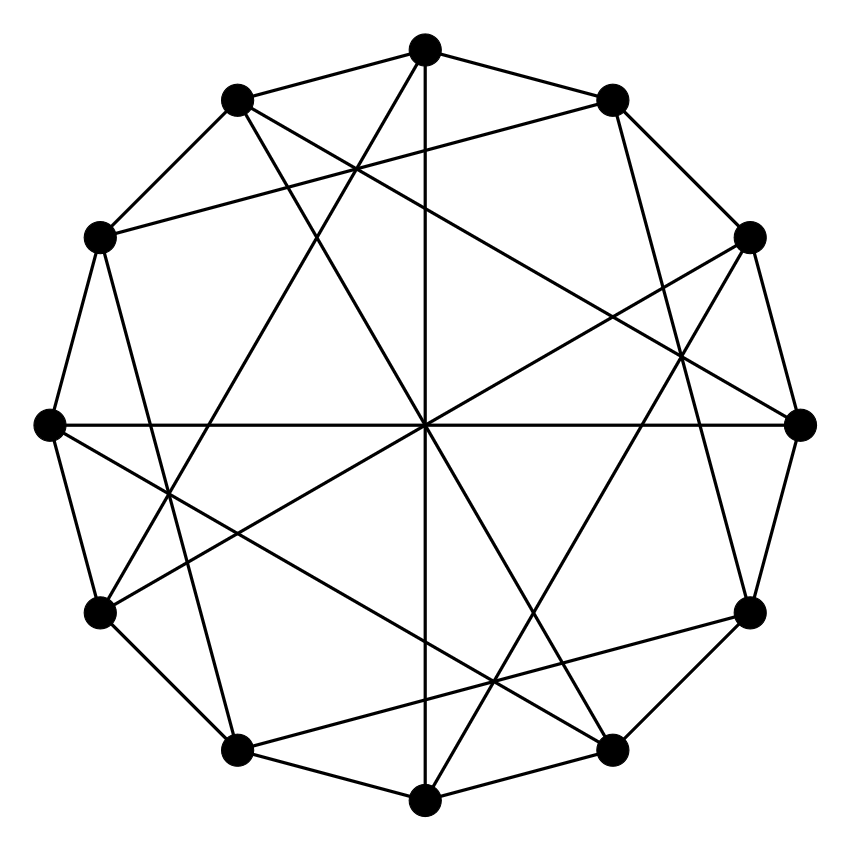
3. feladat. Párosak-e az alábbi gráfok? Amelyik igen, add meg egy két színnel való színezését vagy egy „alsó-felső” lerajzolását (Rád bízom, hogy ki legyen fölül...). Amelyik nem páros, abban adj meg egy páratlan hosszúságú kört. Dolgozhatsz papíron is, de használhatod ezt a játékot is. (Használati utasítás: fent válassz ki egy gráfot, aztán a csúcsokra kattintgatva színezd őket két színnel. A csúcsokat mozgathatod is, hogy „alsó-felső” ábrát kapj. Ha úgy gondolod, hogy nem páros a gráf, akkor az élekre kattintva ki tudsz jelölni páratlan hosszú kört.)
 |
 |
 |
| (a) | (b) | (c) |
 |
 |
 |
| (d) | (e) | (f) |
Megoldás: Három páros gráf van: (a), (d) és (e). A (c) és (f) gráfokban van 5 hosszú kör, a (b) gráfban pedig 9 hosszúságú kört lehet találni.
| előző rész: Hamilton-út és Euler-vonal |  |
következő rész: síkgráfok |