Síkgráfok
1. feladat. Le lehet-e rajzolni a „házikó” gráfot úgy, hogy az élek (vagy pontosabban: az éleket ábrázoló vonalak) ne messék egymást?
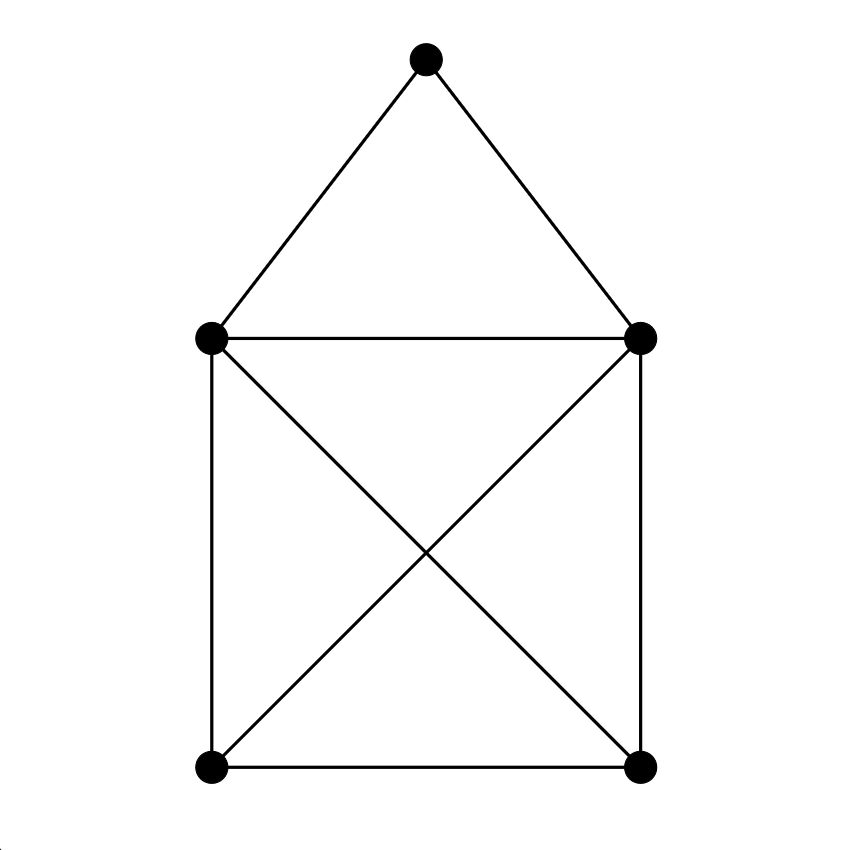
Gráfon továbbra is mindig véges irányítatlan gráfot értünk, amelyben nincsenek se hurokélek se többszörös élek. Mielőtt megnézed a feladatok megoldásait, gondolkozz, és próbáld önállóan megoldani őket, majd vesd össze a megoldást a sajátoddal!
1. feladat. Le lehet-e rajzolni a „házikó” gráfot úgy, hogy az élek (vagy pontosabban: az éleket ábrázoló vonalak) ne messék egymást?

Megoldás: Igen, például így:
Ez nem csalás, mert a gráfoknál csak az számít, hogy melyik csúcs melyikkel van összekötve; az mindegy, hogy ez hogyan van lerajzolva. Kivéve most, mert most pont azzal foglalkozunk, hogy hogyan lehet lerajzolni egy gráfot! Síkgráfoknak nevezzük az olyan gráfokat, amiket le lehet rajzolni a síkon úgy, hogy az éleket jelképező görbék nem metszik egymást. (A „térgráf” fogalma nem lenne túl érdekes, mert térben minden gráfot le lehet rajzolni metszéspontok nélkül. Találd ki, hogy hogyan!) A „házikó” gráf tehát síkgráf.
Egyenes élekkel is le lehet rajzolni; próbáld meg, mielőtt kattintasz!
Nem véletlen, hogy a házikót le lehetett rajzolni egyenes vonalakkal: Fáry István tétele szerint minden síkgráfot le lehet rajzolni egyenes, nem metsző élekkel. Ebben a játékban is a csúcsokat mozgatva, egyenes szakaszokkal kell „síkbarajzolni” a gráfokat. Nem mindegyiket lehet; nézzük meg sorban őket.
2. feladat. Síkráf-e a kocka gráfja?
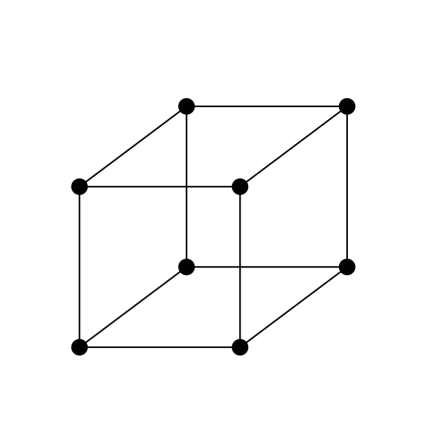
Megoldás: Igen, a kocka gráfja síkgráf. Ez elég könnyű volt, szerintem nem is kell megmutatnom a megoldást.
3. feladat. Síkráf-e a doekaéder gráfja?
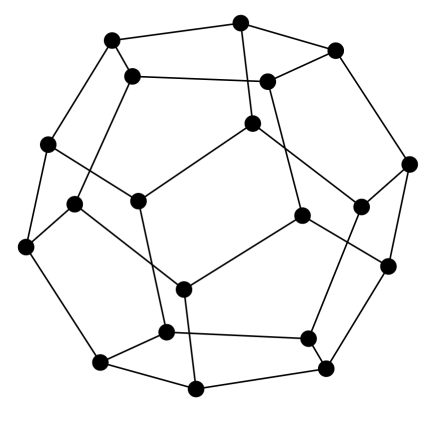
Megoldás: Igen, a dodekaéder gráfja is síkgráf. Íme egy síkbarajzolása:
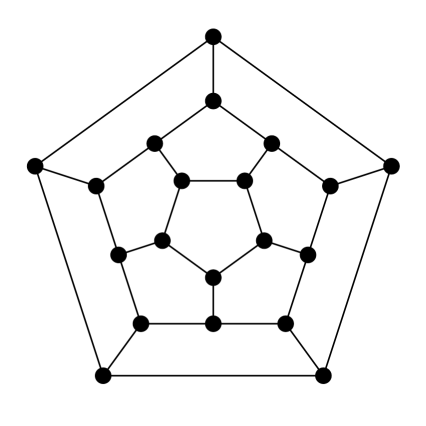
Ez az ábra ismerős lehet: láttuk már a páros gráfos játékban (sőt már a Hamilton-utaknál is). A csúcsok ugyanúgy vannak címkézve a „térbeli” és a síkbeli ábrán; ennek segítségével el tudod rendezni a csúcsokat úgy, hogy a fenti síkbrajzolást kapd.
A kocka és a dodekaéder is konvex poliéder. Minden konvex poliéder élgráfja síkgráf: a poliédert „kifordítva” megkapjuk a gráf egy síkbarajzolását. Az alábbi videó a dodekaéder példáján mutatja ezt.
Az Euler-féle poliédertétel szerint ha egy konvex poliédernek c csúcsa, e éle és l lapja van, akkor l+c=e+2. (Ellenőrizd a kockára és a dodekaéderre.) Ez a tétel általánosítható síkgráfokra: egy összefüggő síkgráf metszéspontok nélküli lerajzolása tartományokra osztja a síkot, és az l+c=e+2 összefüggés érvényben marad, ha most l a tartományok számát jelöli (beleértve a külső, nem korlátos tartományt is). Ez általánosabb, mint a poliédertétel, mert vannak olyan síkgráfok, amelyek nem kaphatóak meg poliéder kiterítéseként (pl. az egyetlen élből álló kétpontú gráf).
4. feladat. Az alábbi gráf neve „három ház-három kút” gráf (jelölése: K3,3). A fölső három csúcs a három ház, az alsó három csúcs a három kút, és az a kérdés, hogy lehet-e mindhárom háztól mindhárom kúthoz egy-egy utat építeni úgy, hogy ne keresztezzék egymást. Vagyis síkráf-e K3,3?

Megoldás: Nem, K3,3 nem síkgráf. Ezt be lehet bizonyítani az Euler-tétel segítségével (K3,3 egy elképzelt lerajzolásában a tartományokat számolgatva), de itt olvasható egy közvetlen bizonyítás is (a 28. oldaltól kezdve).
5. feladat. Síkráf-e az 5 pontú teljes gráf (jelölése: K5)?
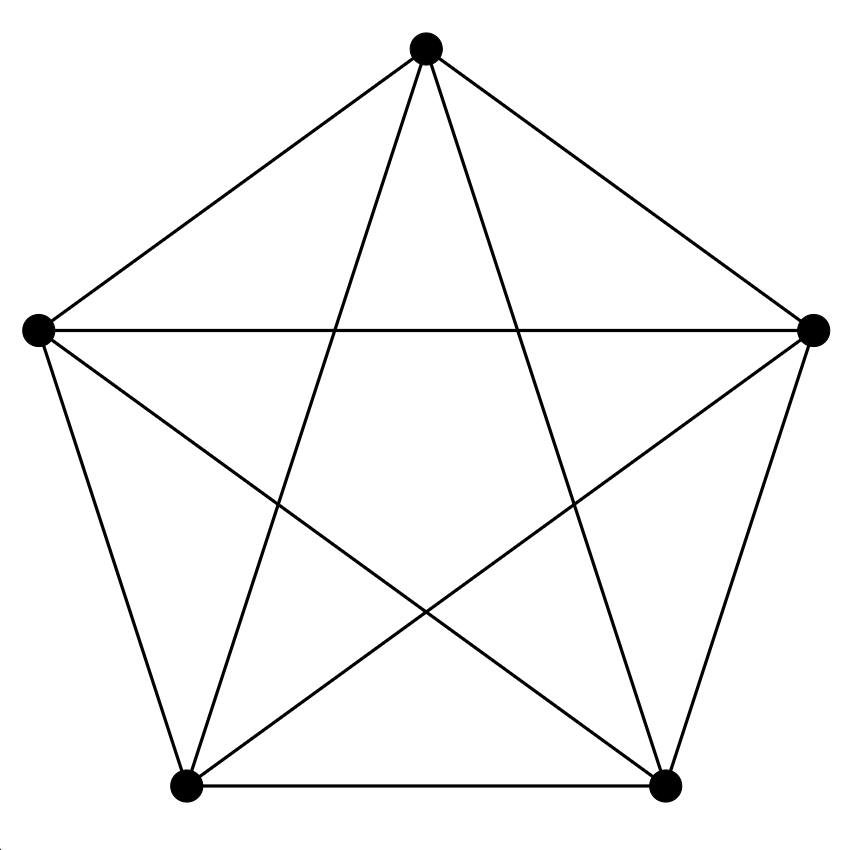
Megoldás: Nem, K5 sem síkgráf. Ezt hasonlóan lehet bizonyítani, mint a K3,3 gráfnál.
A fentiekből következik, hogy ha egy gráf tartalmazza K5-öt vagy K3,3-at (pontosabban ezek valamelyikével izomorf részgráfot), akkor nem lehet síkgráf. Sőt, akkor sem lehet síkgráf, ha olyan gráfot tartalmaz, ami K5-ből vagy K3,3-ból kapható úgy, hogy az élekre újabb csúcsokat helyezünk (felosztjuk őket „rövidebb” élekre), például így:
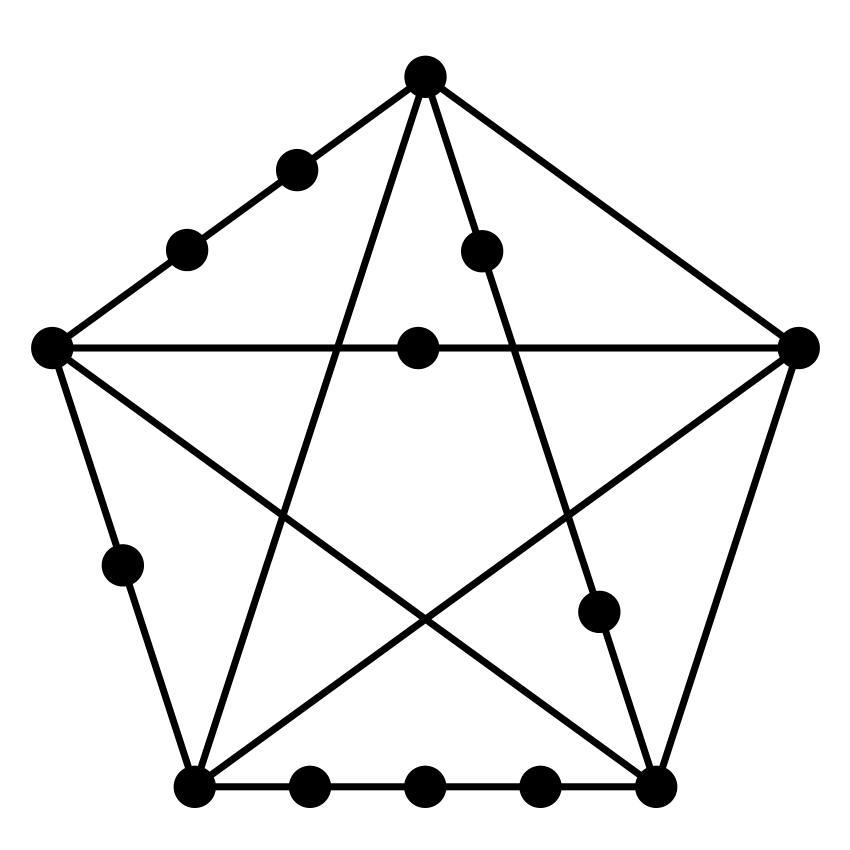
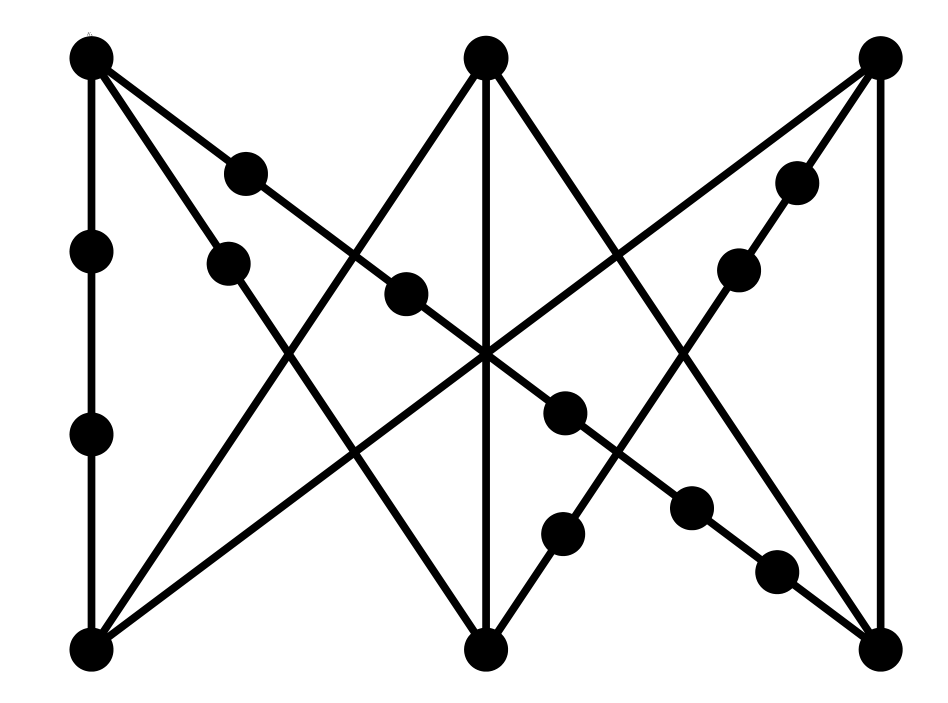
A fenti megfigyelés megfordítása is igaz: ha egy gráf nem síkgráf, azért mindig K5 vagy K3,3 a „felelős”. Ez a mély eredmény Kuratowski tétele: egy gráf akkor és csak akkor síkgráf, ha nem tartalmaz olyan részgráfot, ami megkapható K5-ből vagy K3,3-ból élek felosztásával.
6. feladat. Síkráf-e az alábbi gráf?
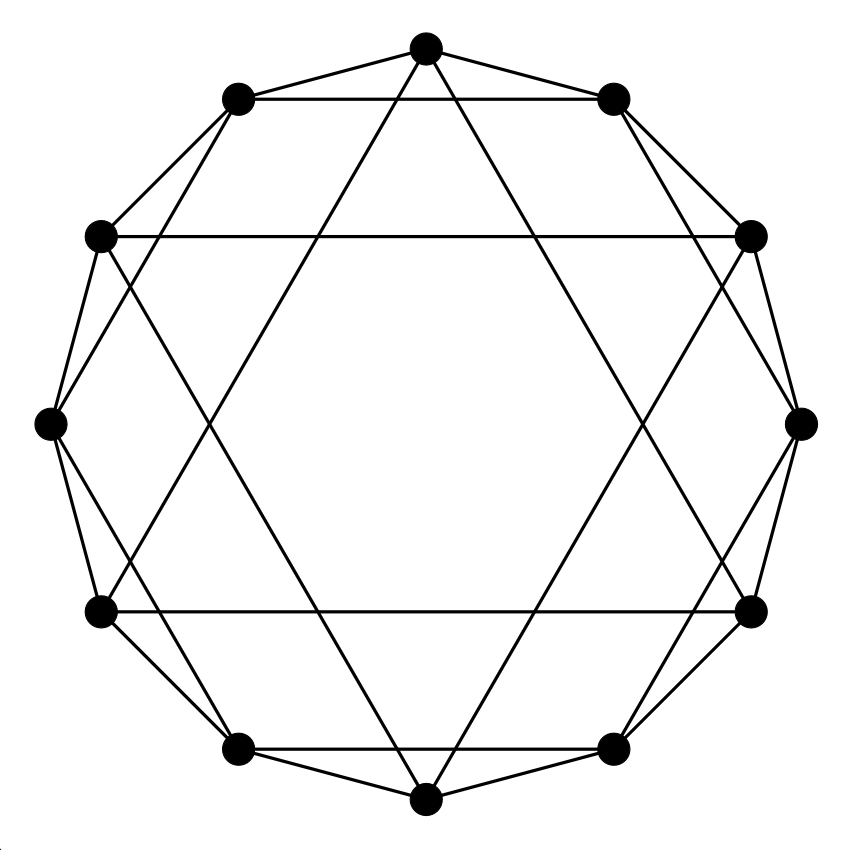
Megoldás: Igen, ez síkgráf. Íme egy síkbarajzolása:
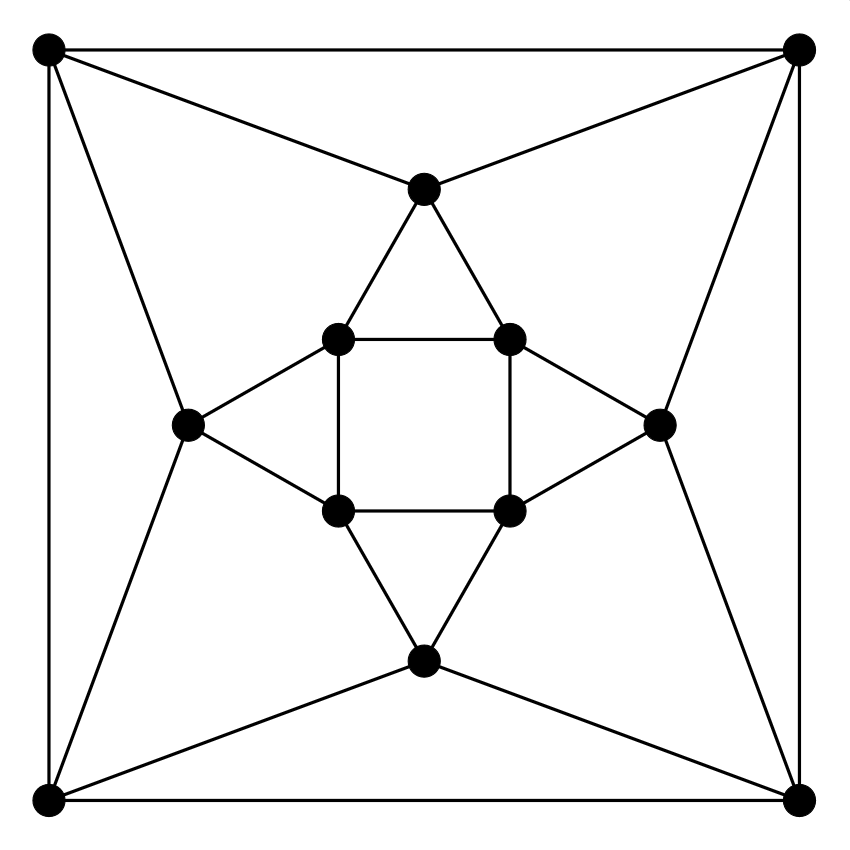
Ez az ábra is ismerős lehet az Euler-vonalas játékból. A csúcsok itt is ugyanúgy vannak címkézve a két játékban; ennek segítségével le tudod ellenőrizni, hogy a két ábrán valóban ugyanaz a gráf szerepel. Egyébként ez is egy poliédernek, nevezetesen a kuboktaédernek a gráfja:
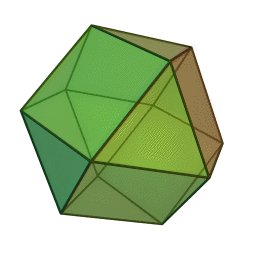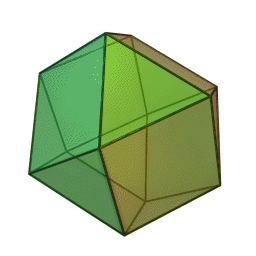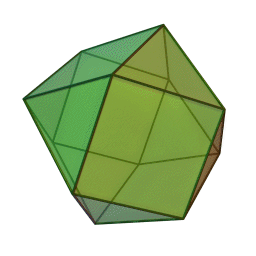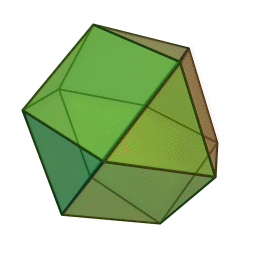
7. feladat. Síkráf-e az alábbi Möbius-létra? (Vajon honnan kapta a nevét?)
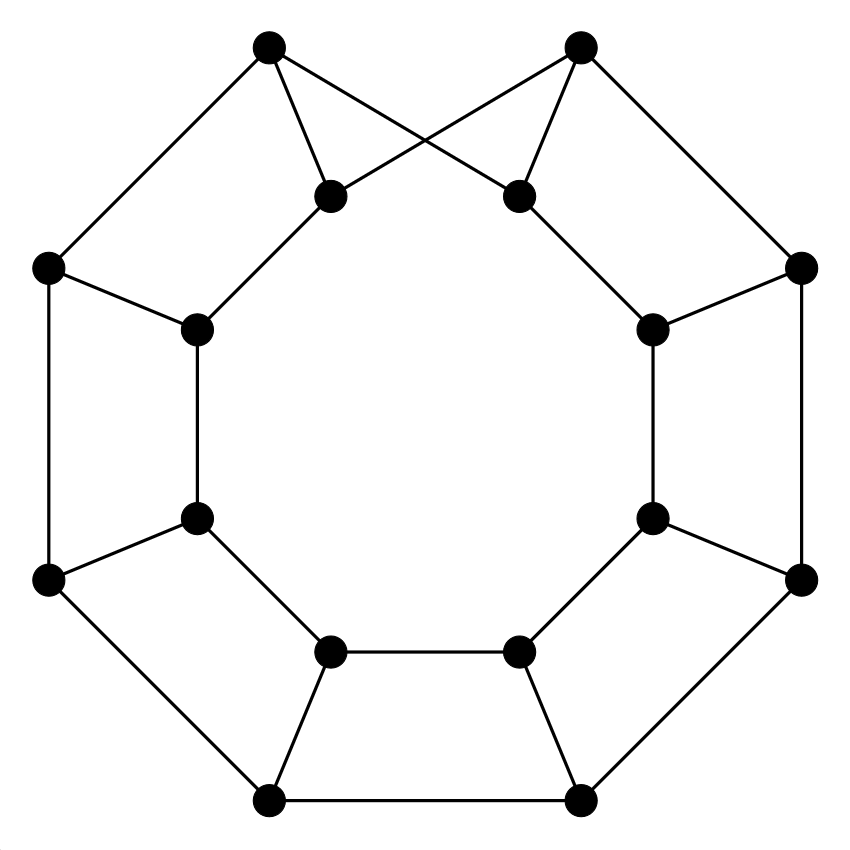
Megoldás: Nem, ez nem síkgráf. Mutatom, hogyan lehet benne megtalálni K3,3 egy felosztását:
8. feladat. Síkráf-e az alábbi gráf?
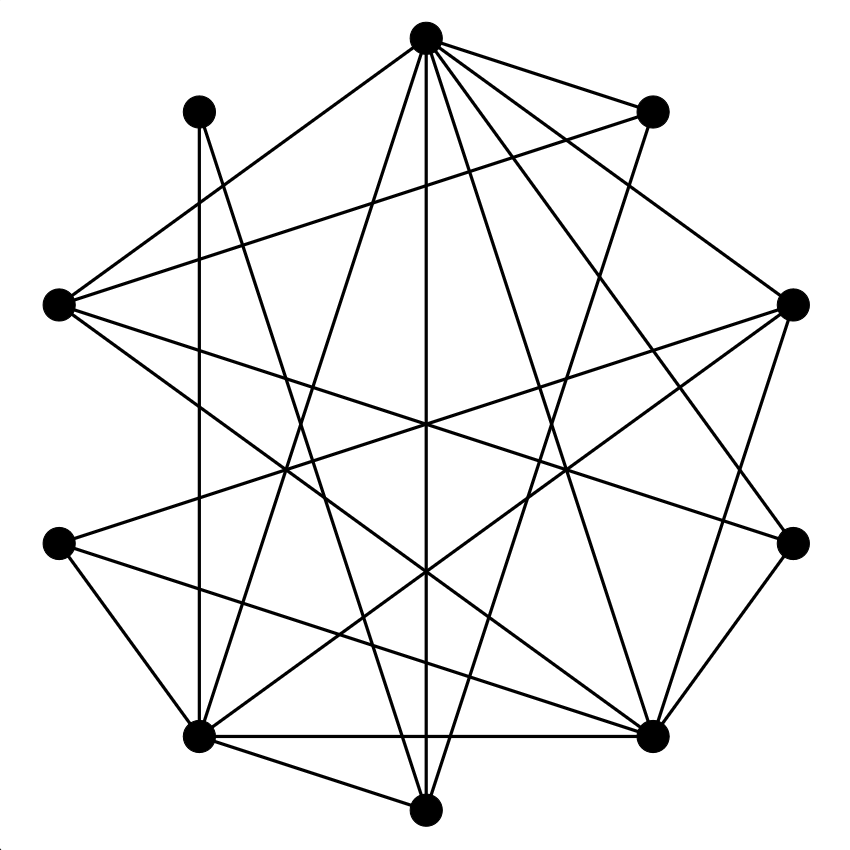
Megoldás: Igen, ez síkgráf. A megoldást nem mutatom meg, csak azt, hogy ebből a játékból származik (készítette: John Tantalo). Az első szintű feladványok könnyebbek mint ez; a felső határ pedig a csillagos ég…
9. (utolsó) feladat. Síkráf-e azalábbi gráf?
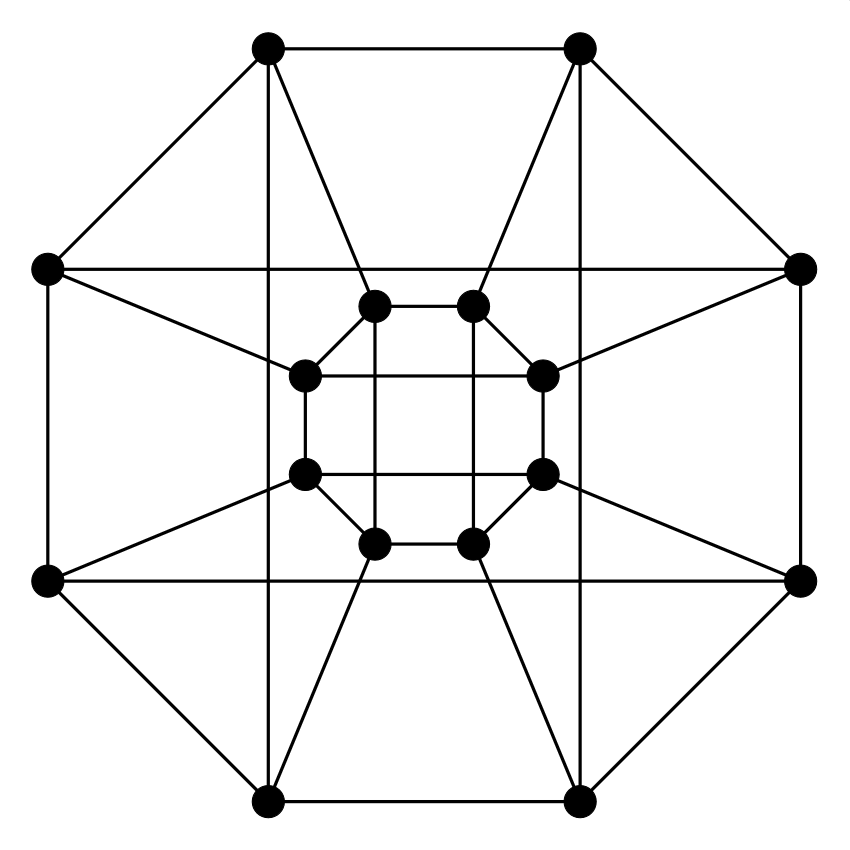
Megoldás: Nem, ez nem síkgráf. Egyébként ez nem más, mint a négydimenziós kocka gráfja:

A páros gráfoknak és a síkgráfoknak látszólag nem sok közük van egymáshoz, de a kettőt összekapcsolják a gráfszínezések. Egy páros gráf csúcsait ki lehet színezni két színnel úgy, hogy ne legyen „monokromatikus” él, azaz egy él két végpontja soha ne legyen ugyanolyan színű. Ha egy gráf nem páros, akkor felmerül a kérdés, hogy ki lehet-e színezni a csúcsokat három színnel; ha nem, akkor esetleg négy színnel, és így tovább. A szükséges színek minimális számát a gráf kromatikus számának nevezzük. Egy gráf párosságát, vagyis 2-színezhetőségét könnyű eldönteni: bárhogy kezd el színezni az ember, ha a gráf tényleg páros, akkor ki fog jönni. A 3-színezhetőség már jóval nehezebb probléma; itt előfordulhat, hogy zsákutcába jutunk, és elő kell venni a negyedik színt is, pedig ha ügyesebben kezdtük volna, akkor elég lett volna három szín is. A Hamilton-körökhöz hasonlóan ez sem szubjektív nehézség: bizonyított tény, hogy NP-teljes probléma eldönteni egy gráfról, hogy kiszínezhető-e három színnel.
A síkbarajzolós játékban többször kattintva egy csúcsra négy szín között tudsz váltogatni (sőt, ötödik színként használhatod az eredeti fehér színt is), így megpróbálhatod a gráfokat kiszínezni a lehető legkevesebb színnel. (A játékban szereplő gráfok között csak egy van, amihez öt szín kell. Melyik az?) Nevezetes tény, hogy egy síkgráf színezéséhez mindig elég négy szín; népszerűbb megfogalmazásban: minden térképen ki lehet színezni az országokat négy színnel úgy, hogy a szomszédos országok különböző színűek legyenek. Ezt már 1852-ben megsejtette Francis Guthrie, de a bizonyításra több, mint 100 évet kellett várni: a négyszín-tételt 1976-ban bizonyította Kenneth Appel és Wolfgang Haken. Ez volt az egyik első számítógéppel segített bizonyítás: Appel és Haken „humán erőforrással” (gondolkozással) visszavezette a végtelen sok lehetséges síkgráf színezését 1834 esetre, majd azokat számítógéppel egyenként megvizsgálták (1200 óráig futott a program).
| előző rész: páros gráfok |  |
következő rész: fák és erdők |