Gráfon továbbra is mindig véges irányítatlan gráfot értünk, amelyben nincsenek se hurokélek se többszörös élek. Mielőtt megnézed a feladatok megoldásait, gondolkozz, és próbáld önállóan megoldani őket, majd vesd össze a megoldást a sajátoddal!
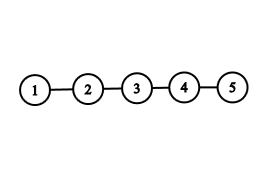
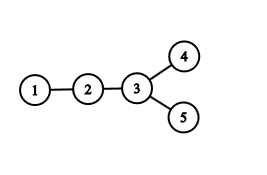
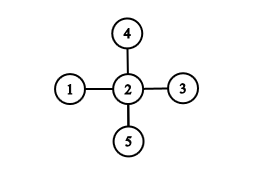
1. feladat. Rajzolj 5 pontot, és húzz be minél kevesebb élt úgy, hogy összefüggő gráfot kapj. Hány élt kellett behúznod?
Megoldás: Négy éllel meg lehet csinálni, annál kevesebbel nem. Izomorfia erejéig három megoldás van (próbáld megkeresni mindet, mielőtt kattintasz!):
Ahogy korábban is, az ábrákra kattintva megkapod az élek listáját, amit bemásolva a CS Academy Graph Editor oldalán bal oldalt a „Graph Data” mezőbe (az eredetileg ott lévő adatokat kitörölve), le tudod ellenőrizni, hogy a megoldásaid valóban izomorfak a fentiekkel.
2. feladat. Rajzolj 5 pontot, és húzz be minél több élt úgy, hogy a gráfban ne keletkezzen kör. Hány élt kellett behúznod?
Megoldás: Négy élt még be lehet húzni úgy, hogy körmentes gráfot kapjunk, de többet nem. Izomorfia erejéig három megoldás van (próbáld megkeresni mindet, mielőtt kattintasz!):
Feltűnhet, hogy ugyanazok a gráfok jöttek ki mindkét feladatnál. Ez nem véletlen. Az első feladatban minimális összefüggő gráfot rajzoltunk, a másodikban maximális körmentes gráfot. Meg lehet mutatni, hogy ez a két tulajdonság ekvivalens. A bizonyítást elolvashatod az az előadás anyagában (2809–2848. old.). Ezeket a gráfokat fáknak nevezzük. A fák tehát az összefüggőség és a körmentesség „határmezsgyéjén” helyezkednek el: már éppen elég sok élük van ahhoz, hogy összefüggőek legyenek, de még épp elég kevés élük van, hogy ne legyen bennük kör.
A két feladatban konstruált ötpontú fáknak négy élük volt. Ez sem véletlen: egy n csúcsú fának mindig n-1 éle van. Sőt, be lehet bizonyítani, hogy ez a tulajdonság az összefüggőség vagy a körmentesség bármelyikével együtt pontosan a fákra teljesül. Összefoglalva:
3. feladat. Rajzolj minél több 6 pontú fát. Izomorfia erejéig hány fát tudtál rajzolni?
Megoldás: Izomorfia erejéig hat megoldás van (próbáld megkeresni mindet, mielőtt kattintasz!):
Gyakorlásként oldd még meg a gráfelmélet feladatsorból a 3.11. feladatot. És íme még négy gondolkoznivaló:
És ha nagyon ráérsz: Hány 7 pontú fa van izomorfia erejéig?
Nem túl meglepő módon, erdőnek olyan gráfot nevezünk, ami néhány fából áll. Precízebben: erdőn körmentes gráfot értünk (hiszen ennek az összefüggő komponensei fák). Megengedjük azt is, hogy csak egy komponens legyen, tehát egyetlen fa is erdőnek számít.
4. feladat. Rajzolj minél több 3 pontú erdőt. Izomorfia erejéig hány erdőt tudtál rajzolni?
Megoldás: Izomorfia erejéig három megoldás van (próbáld megkeresni mindet, mielőtt kattintasz!):
5. feladat. Hány fából állhat egy olyan erdő, aminek 10 csúcsa és 7 éle van?
Megoldás: Mivel minden fában eggyel kevesebb él van, mint ahány csúcs, az erdőnk 10-7=3 fából áll.
Részletesebben és formálisabban: Jelöljük x-szel a fák, vagyis az összefüggő komponensek számát. Legyen a komponensekben rendre n1, n2, … ,nx csúcs. Mivel összesen 10 csúcs van, n1+n2+⋯+nx = 10. Az egyes komponenseknek rendre n1-1, n2-1, … nx-1 éle van (hiszen mindegyik fa). Mivel összesen 7 él van, (n1-1)+(n2-1)+⋯+(nx-1) = 7. Node (n1-1)+(n2-1)+⋯+(nx-1) = n1+n2+⋯+nx - x = 10 - x. Ebből kapjuk, hogy x = 3.
Gyakorlásként oldd még meg a gráfelmélet feladatsorból a 3.9. feladatot.
| előző rész: síkgráfok |  |
következő rész: párosítások |