Gráfon továbbra is mindig véges irányítatlan gráfot értünk, amelyben nincsenek se hurokélek se többszörös élek. Mielőtt megnézed a feladatok megoldásait, gondolkozz, és próbáld önállóan megoldani őket, majd vesd össze a megoldást a sajátoddal!
1. feladat. A múlt héten szó volt egy 6 fős társaságról, ahol mindenki 4 másik embert ismer. Egyikük hallott egy szaftos pletykát, elmondja hát valamelyik ismerősének, az továbbadja egy másik ismerősnek, és így tovább. Lehetséges-e, hogy előbb-utóbb mindenkihez eljut a pletyka? (Mindenki csak egy ismerősének adja tovább a pletykát, méghozzá olyannak, aki még nem hallotta.)
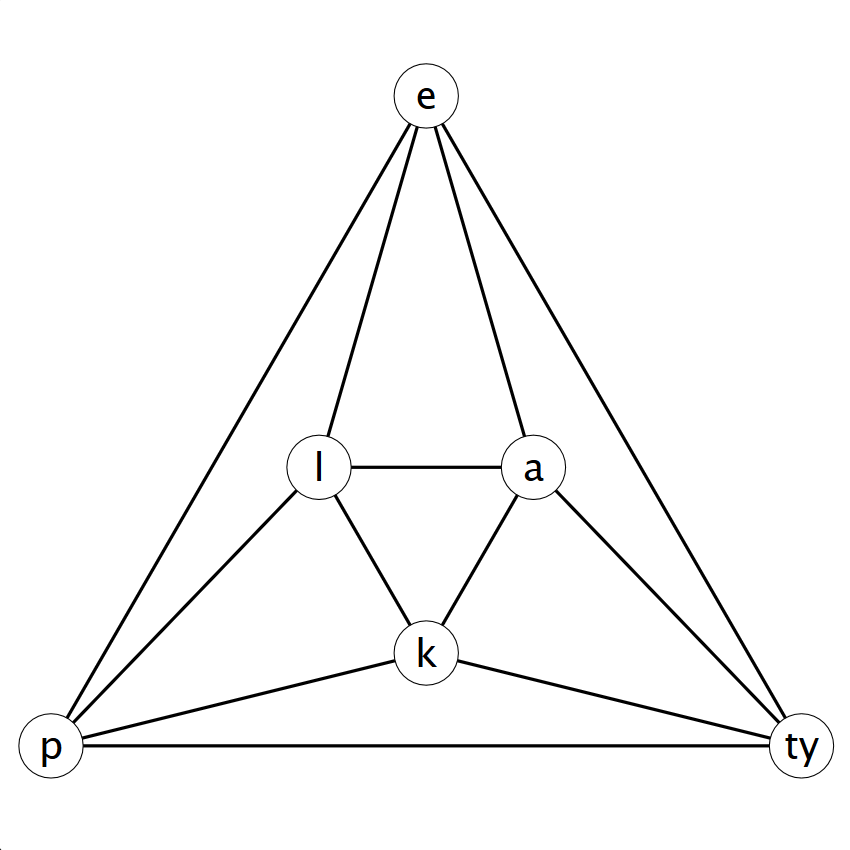
Megoldás: A múlt heti első feladatban láttuk, hogy az ismeretségeket leíró gráf lényegében (izomorfia erejéig) egyértelmű, mégpedig így fest:
A pletyka terjedési útját a gráfban – nem túl meglepő módon – egy út írja le. Az a kérdés, van-e ebben a gráfban olyan út, ami minden csúcson áthalad.
Igen, van, íme:
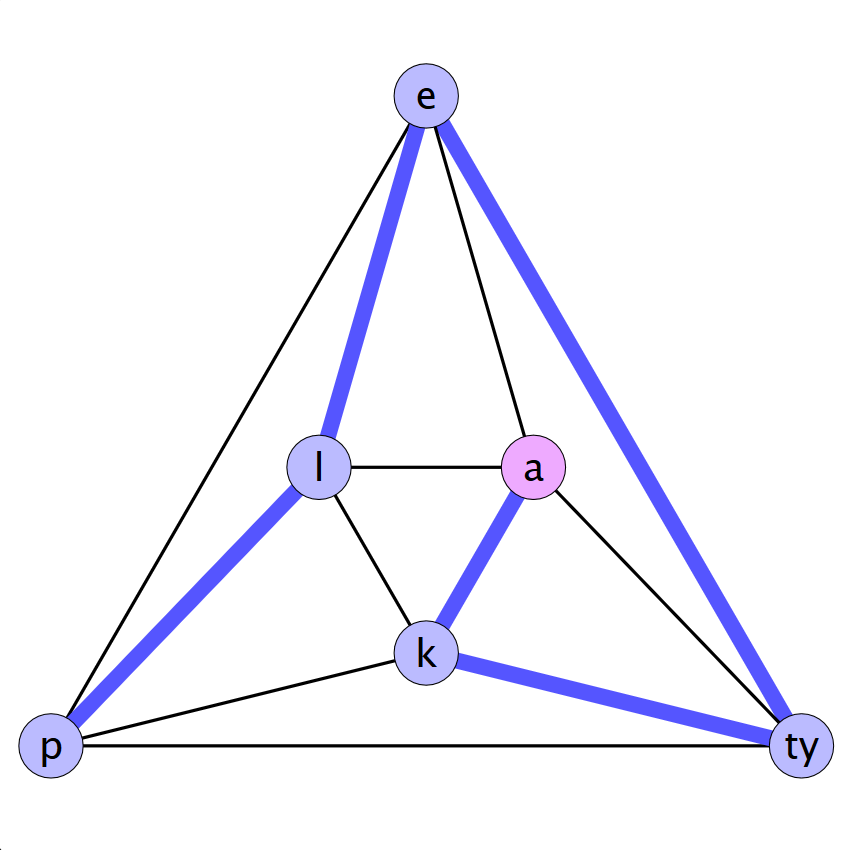p → l → e → ty → k → a
Az ilyen utat, ami egy gráf minden csúcsán áthalad (és, út lévén, minden csúcson csak egyszer halad át), Hamilton-útnak nevezzük.
2. feladat. Az előző feladatban szereplő társaságnak focizni támadt kedve. Tudják-e úgy körbepasszolni a labdát, hogy mindenkihez pontosan egyszer jusson el, mire körbeér? (Természetesen mindenki csak ismerős embernek passzol.)
Megoldás: Igen, például így:
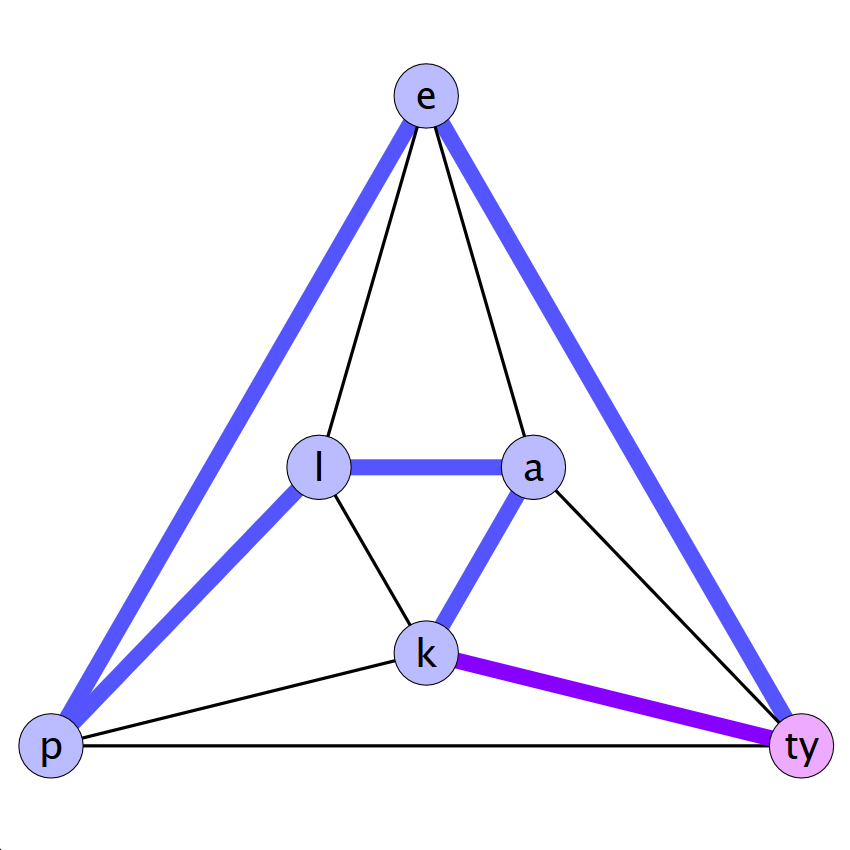k → a → l → p → e → ty → k
Az ilyen kört, ami egy gráf minden csúcsán áthalad (és, kör lévén, minden csúcson csak egyszer halad át, ha nem számítjuk azt, hogy a kezdő- és végpont ugyanaz, már ha egyáltalán meg akarjuk mondani, hogy hol „kezdődik” a kör), Hamilton-körnek nevezzük.
Ha egy gráfban van Hamilton-kör, akkor persze Hamilton-út is van: a Hamilton-körből egy tetszőleges élt elhagyva Hamilton-utat kapunk. Például a fenti ábrán a lila él elhagyásával a k → a → l → p → e → ty Hamilton-utat kapjuk (ez is jó lett volna az 1. feladat megoldásának, és van még sok más Hamilton-út is).
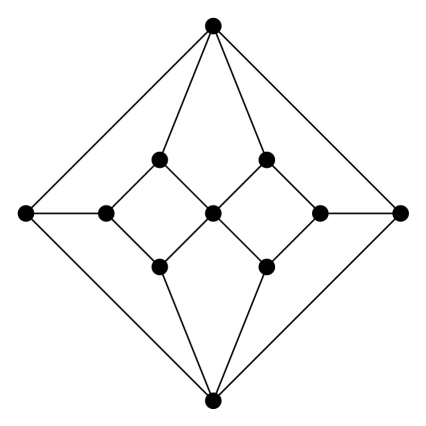
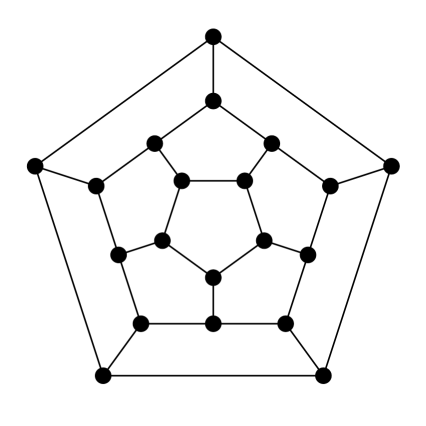
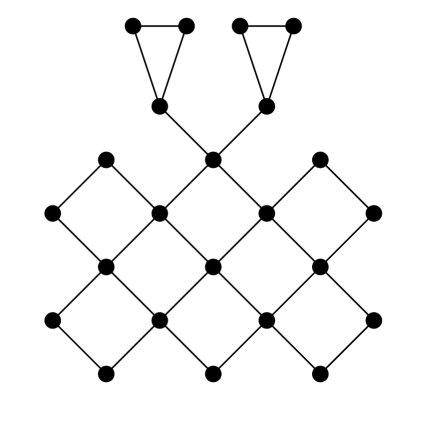
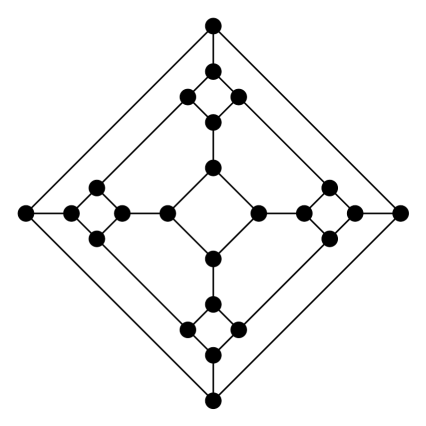
3. feladat. Keress Hamilton-utat az alábbi gráfokban. Dolgozhatsz papíron is, de használhatod ezt a játékot is. (Használati utasítás: fent válassz ki egy gráfot, aztán a csúcsokra kattintgatva kezdj utat építeni. Ha elakadtál, a legutolsó (lila) csúcsot ki tudod törölni, ha rákattintasz. Ha elölről szeretnéd kezdeni, akkor kattints újra odafent a gráf ikonjára.) A hat gráf között van egy, amelyikben nincs Hamilton-út, az összes többiben van (a legtöbben még Hamilton-kör is).
 |
 |
 |
| (a) | (b) | (c) |
 |
 |
 |
| (d) | (e) | (f) |
Melyik az a gráf a hat közül, amelyikben nincs Hamilton-út?
Hogy a (d) gráfban miért nincs Hamilton-út, arra nem elég meggyőző indoklás az, hogy „sokáig próbálkoztam, és nem találtam”. Tudnál valami rövid, frappáns indoklást adni?
Íme egy lehetséges magyarázat: a (d) gráfban van olyan csúcs, amit kitörölve 3 részre esik szét a gráf (melyik csúcs ez?). Ha lenne benne Hamilton-út, akkor egy csúcs elhagyásával legfeljebb két összefüggő komponenst kaphatnánk (ha az egész gráf csak a Hamilton-útból állna, akkor is csak két részre eshetne).
A (b) gráfban van Hamilton-út, de nincs Hamilton-kör. (A többiben van Hamilton-kör, persze a (d) kivételével. Ha eddig olyan Hamilton-utakat találtál, amik nem körök, akkor próbáld most megkeresni a Hamilton-köröket.) Gondolkozz el rajta, hogy miért nincs a (b) gráfban Hamilton-kör! Erre a kérdésre később még visszatérünk.
A (d) gráffal kapcsolatban adtunk egy szükséges feltételt Hamilton-út létezésére (kevés csúcs elhagyásával ne essen szét sok részre). Ismertek elegendő feltételek is, pl. Dirac tétele szerint ha minden csúcs össze van kötve a csúcsoknak legalább a felével, akkor a gráfban van Hamilton-kör (feltéve, hogy legalább 3 pontja van). Egyszerű szükséges és elegendő feltétel azonban nem ismert, és nem is várható, hogy ilyet valaha felfedeznek, mert a Hamilton-út létezésének eldöntése bizonyítottan nehéz probléma (az ún. NP-problémaosztályban a lehető legnehezebb). Marad tehát a keresgélés, annak sikertelensége esetén pedig olyan ad hoc bizonyítékok kitalálása, mint a (d) példánál.
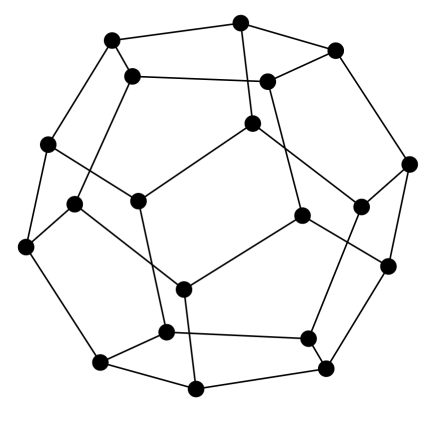
A Hamilton-út William Rowan Hamilton XIX. századi ír matematikusról kapta a nevét. Ő találta ki az Icosian game nevű játékot, ahol a fenti (c) gráfban kell Hamilton-kört keresni. Itt látható a játék (megoldott állapotban):
4. feladat. Az 1. és 2. feladatban említett társaság megszomjazott focizás közben, ezért inni fognak, de közben a focizást sem hagyják abba. Mindenki ismerős embernek passzol, és a sikeres passz örömére koccintanak. Meg tudják-e ezt úgy tenni, hogy mindenki minden ismerősével pontosan egyszer koccintson? (Most persze egy emberhez többször is kerülhet a labda, de mindig mástól kapja.)
Megoldás: Igen, például így (a Hamilton-úttal ellentétben, a kész ábrából nem látszik, hogy milyen sorrendben történtek a koccintások, ezért videóban mutatom):
p → l → e → ty → k → a → l → k → p → e → a → ty → p
A fenti videón az látszik, hogy a gráfot le lehet rajzolni egy vonallal, a ceruza felemelése nélkül. Gráfelméleti nyelven megfogalmazva arról van szó, hogy olyan sétát tettünk, ami a gráf minden élén pontosan egyszer halad át (csúcsok ismétlődhetnek, ezért nem útról, hanem sétáról beszélünk, de élek nem ismétlődhetnek). Az ilyen sétát Euler-vonalnak nevezzük. Ha a séta ugyanoda ér vissza, ahonnan elindult, akkor zárt Euler-vonalról beszélünk.
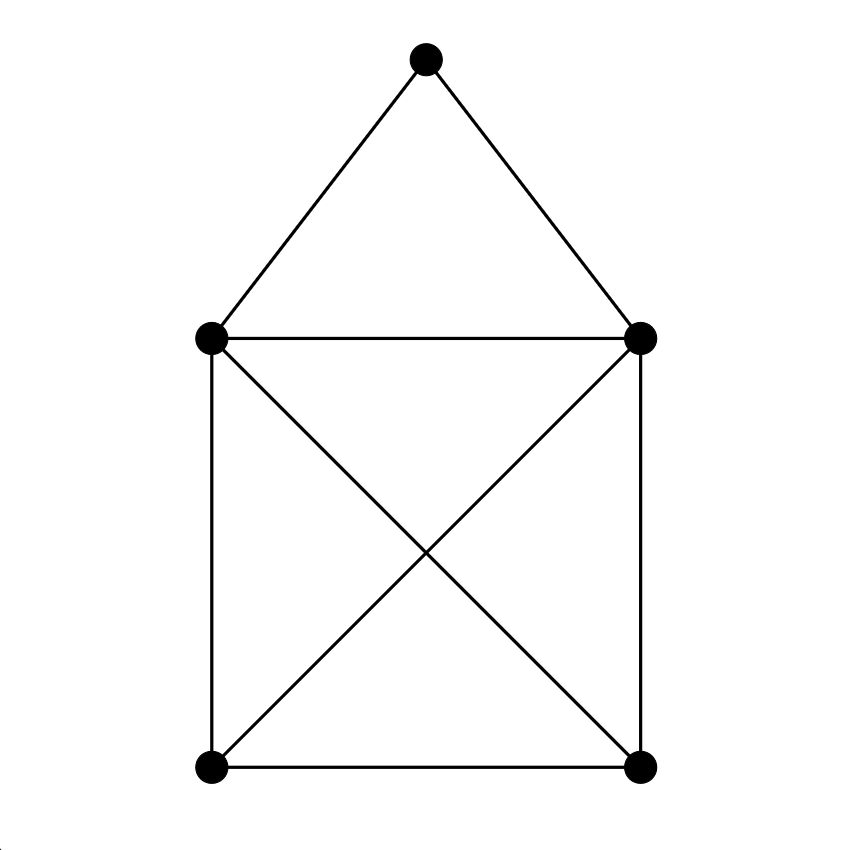
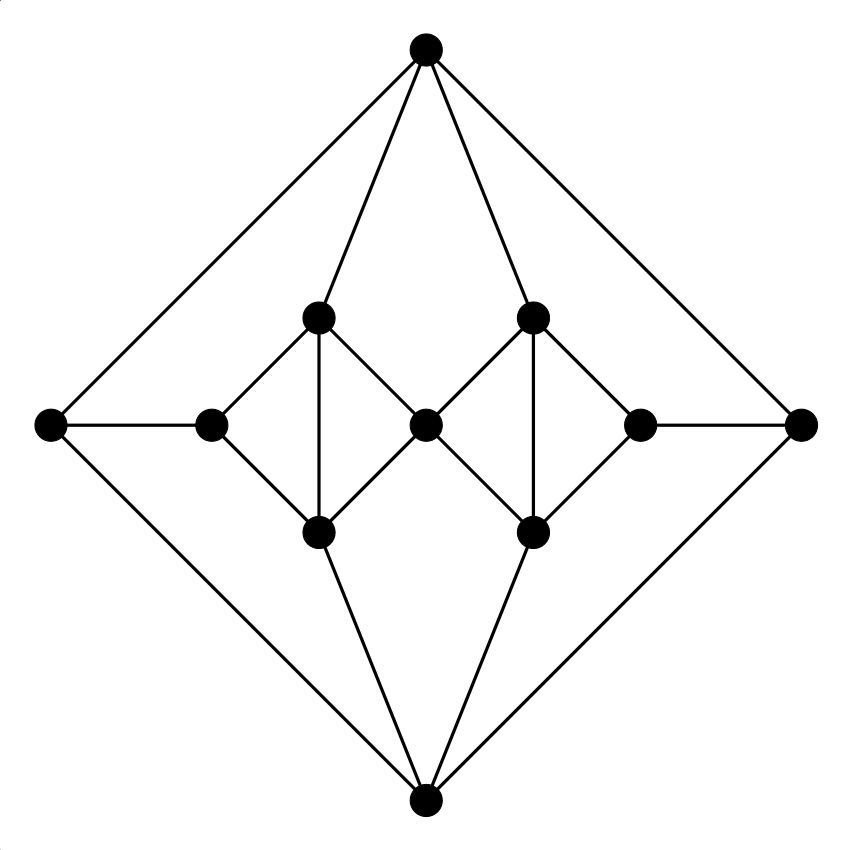
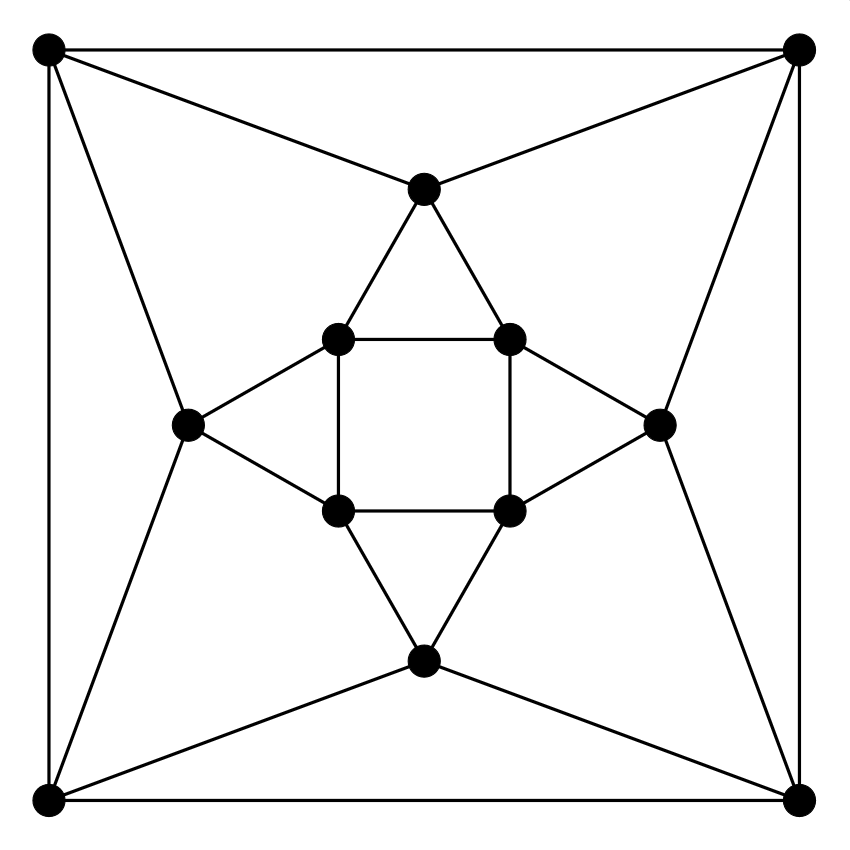
5. feladat. Keress Euler-vonalat az alábbi gráfokban. Dolgozhatsz papíron is, de használhatod ezt a játékot is. (Használati utasítás: fent válassz ki egy gráfot, aztán az élekre kattintgatva kezdj vonalat (élismétlések nélküli sétát) építeni. Ha elakadtál, a legutolsó (lila) élt ki tudod törölni, ha rákattintasz. Ha elölről szeretnéd kezdeni, akkor kattints újra odafent a gráf ikonjára.) A hat gráf között van egy, amelyikben nincs Euler-vonal, az összes többiben van (némelyikben zárt, némelyikben nem zárt).
 |
 |
 |
| (a) | (b) | (c) |
|
 |
 |
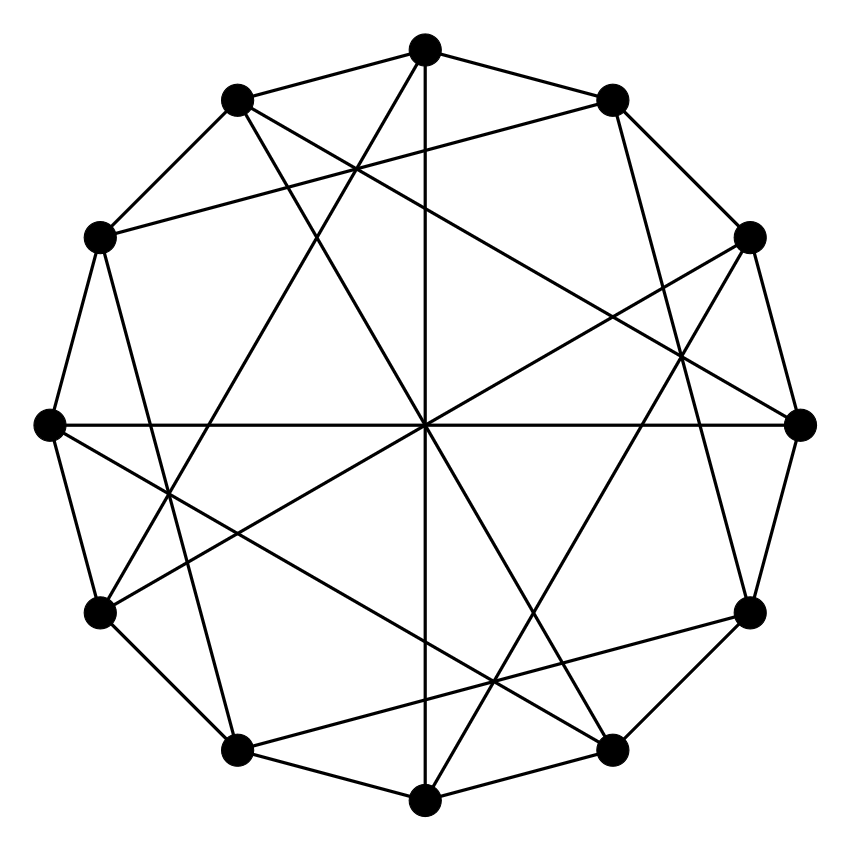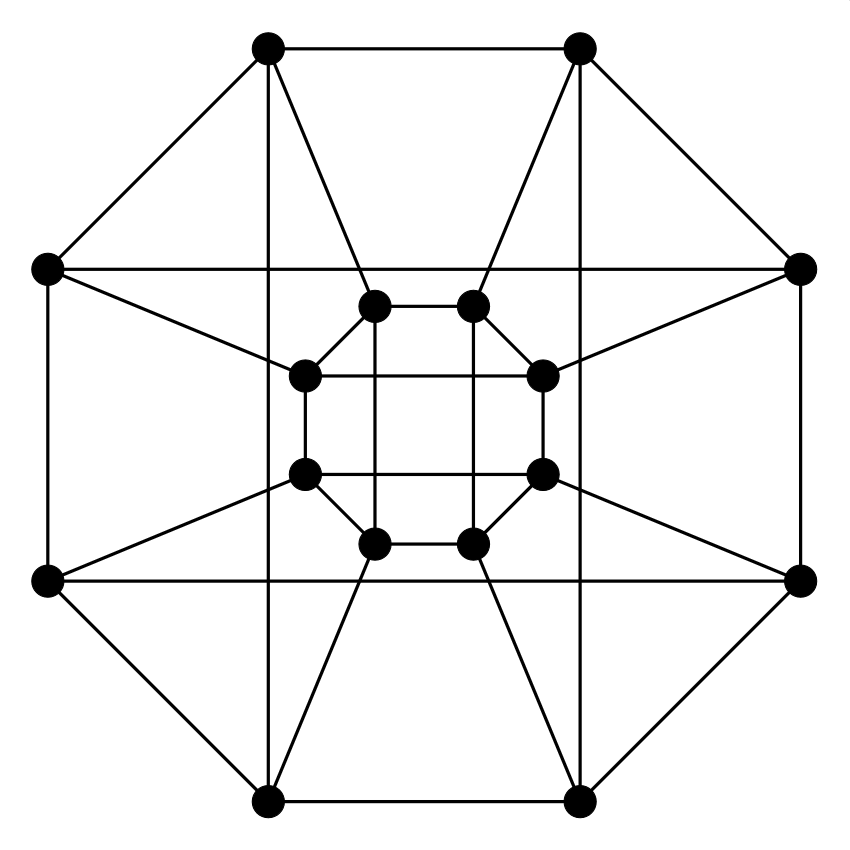| (d) | (e) | (f) |
Melyik az a gráf a hat közül, amelyikben nincs Euler-vonal?
Itt sem elég meggyőző indoklás az, hogy a (b) gráfban hosszú keresgélés után sem találtunk Euler-vonalat. Próbálj valami egyszerű és meggyőző magyarázatot adni!
Ha egy gráfot egy vonallal le tudunk rajzolni, akkor a vonal két végpontja kivételével minden pont foka páros (valahányszor bemegyünk egy csúcsba, mindannyiszor el is kell hagynunk, hacsak nem a vonal valamelyik végpontjáról van szó). A (b) gráfban viszont a páratlan fokú csúcsok száma négy, tehát ezt csak olyan vonallal lehetne lerajzolni, aminek négy vége van.
A fenti magyarázat persze nem csak a (b) gráfra érvényes: ha egy gráfban van Euler-vonal, akkor legfeljebb két páratlan fokú csúcsa lehet. Kevésbé triviális, de megmutatható, hogy ez a fokszámfeltétel nemcsak szükséges, de elegendő is az Euler-vonal létezéséhez. A bizonyítás elolvasható az előadás anyagában; az Euler-vonalas rész a 2731. oldalon kezdődik. Íme tehát az Euler-vonallal rendelkező gráfokat leíró tétel:
Keresztkérdés: Úgy tűnik, a fenti listából kimaradt az az eset, amikor csak egyetlen páratlan fokú csúcs van. Mi a helyzet ezzel az esettel?
A Hamilton-utakkal ellentétben tehát az Euler-vonal létezését eldönteni igen egyszerű: elég a csúcsok fokszámait megnézni. Már csak egy kérdés maradt: Ha a fokszámok alapján úgy látjuk, hogy van Euler-vonal, akkor hogyan találjuk azt meg? Ez is sokkal könnyebb, mint a Hamilton-út esetén, gyakorlatilag nem lehet elrontani, soha nem kell a készülő vonalat visszabontani, és másfelé keresgélni. Több hatékony algoritmus is létezik Euler-vonal megkonstruálására, az alábbi videó a Hierholzer-algoritmust mutatja be. A videót Alejandro Morales készítette, én csak a magyar feliratot adtam hozzá (nem az angol szöveg hű fordítása). Az eredeti videó itt található a YouTube-on. (A bevezető szöveg után 0:30-nál kezdődik maga az algoritmus.)
Próbáld ki az algoritmust az 5. feladatbeli gráfokra!
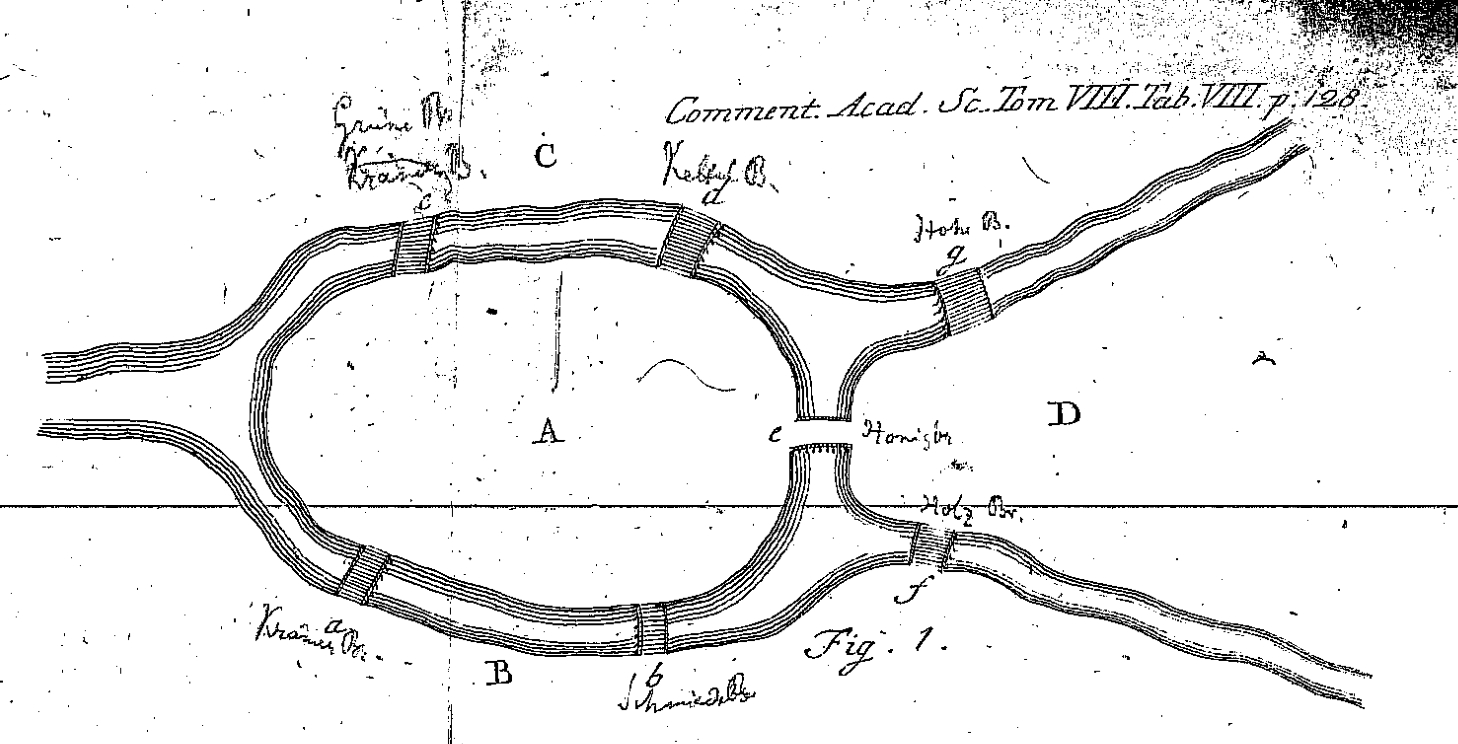
Az Euler-vonal Leonhard Euler XVIII. századi svájci matematikusról kapta a nevét. Ő oldotta meg 1736-ban a königsbergi hidak problémáját; ezt szokták a gráfelmélet megszületésének tekinteni. A problémát itt nem írom le, de az az előadás anyagában; el lehet olvasni a 2731. oldaltól kezdve. Illusztrációként íme a königsbergi hidakat mutató ábra Euler Solutio problematis ad geometriam situs pertinentis című 1736-os cikkéből, amelyben a megoldást ismertette:
| előző rész: gráfelméleti alapfogalmak |  |
következő rész: páros gráfok |