A szükséges alapfogalmakat olvasd el az az előadás anyagában a 2628–2730. oldalakon. A megértést segíthetik az alábbi mateking videók:
A harmadik videó a címével ellentétben nem elég precíz: irányítatlan gráfot definiál, de nem szimmetrikus relációt ad meg. A valóban precíz definíciót lásd az előadás anyagában! A továbbiakban gráfon mindig véges irányítatlan gráfot értünk, amelyben nincsenek se hurokélek se többszörös élek. Mielőtt megnézed a feladatok megoldásait, gondolkozz, és próbáld önállóan megoldani őket, majd vesd össze a megoldást a sajátoddal!
1. feladat. Lehetséges-e, hogy egy 6 emberből álló társaságban mindenki pontosan 4 másik embert ismer?
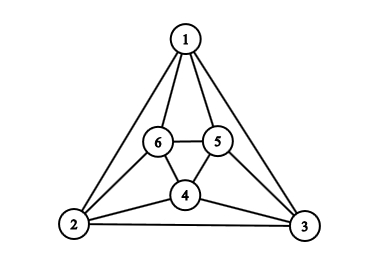
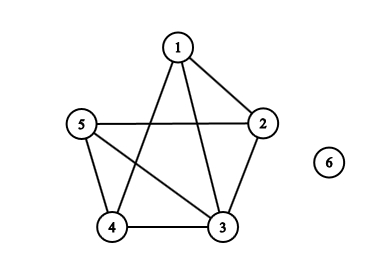
Megoldás: Igen, lehetséges; íme néhány gráf, amik az ismeretségi relációt szemléltetik:
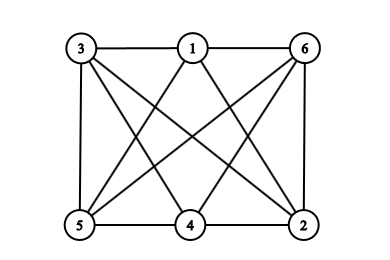
Az első két ábra ugyanazt a gráfot ábrázolja; pontosan ugyanazok a csúcsok vannak összekötve mindkettőben. Erről meggyőződhetsz úgy, hogy felsorolod mindkét gráf éleit, és látni fogod, hogy ugyanazt a 12 élt kapod. Egy másik, kevésbé unalmas lehetőség a következő. Az első ábrára kattintva megnyithatsz egy txt fájlt, amely a gráf éleit tartalmazza. Másold ki ennek a tartalmát, és illeszd be a CS Academy Graph Editor oldalán bal oldalt a „Graph Data” mezőbe (az eredetileg ott lévő adatokat kitörölve). Ekkor megjelenik a gráf, aminek a csúcsait a program megpróbálja automatikusan úgy elhelyezni, hogy jól nézzen ki. Jobb oldalt fölül kattints az „Edit” feliratra, és akkor Te tudod mozgatni a csúcsokat. Állítsd be először úgy őket, hogy a fenti három ábra közül az elsőt kapd, aztán pedig úgy is, hogy a második ábrát kapd. Ezzel meggyőződhettél róla, hogy a két gráf ugyanaz, csak másképp vannak lerajzolva. Épp ez a lényege a gráfoknak: nem az számít, hogy vannak lerajzolva, hanem csak az, hogy melyik csúcs melyikkel van összekötve. A számítógép nem is rajzként tárolja a gráfot, hanem számpárok listájaként (amit beillesztettél a txt fájlból). A gráf matematikai definíciója is elempárok halmazaként adja meg az éleket; a rajz csak szemléltetésre szolgál.
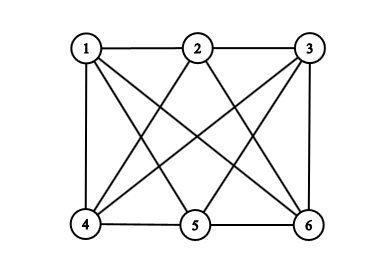
A harmadik ábra nagyon hasonlít a másodikra, de nem ugyanaz a gráf, mert pl. a harmadiknál 1 és 4 össze van kötve, de a másodiknál nincs. Mégis, úgy érezzük, hogy a két gráf „majdnem” ugyanaz: teljesen egyforma a szerkezetük, csak másképp vannak megszámozva a csúcsaik. Ezt szaknyelven úgy fejezzük, ki, hogy a két gráf izomorf. Általában nem könnyű két gráfról eldönteni, hogy izomorfak-e; pl. a fenti ábrán az első és a harmadik gráfról talán ránézésre nem mondanánk meg, hogy izomorfak, ha nem lenne ott köztük segítségként a második ábra. Nagy gráfok esetén még számítógéppel is bajos eldönteni, hogy két gráf izomorf-e.
Ennek a feladatnak izomorfia erejéig egy megoldása van (gondold meg, hogy miért!). Tehát bármilyen gráfot kaptál is, az izomorf a fenti gráfokkal. Ezt ellenőrizheted úgy, hogy a CS Academy Graph Editor oldalán úgy húzogatod a csúcsokat, hogy azt az ábrát kapd, amit Te rajzoltál a feladat megoldásaként (ignorálva a csúcsok számozását, már ha egyáltalán megszámoztad a csúcsokat).
2. feladat. Adj meg olyan 6 csúcsú gráfokat (minél többet), amelyekben a csúcsok fokszámai a következők: 2,2,2,2,4,4.
Megoldás: Izomorfia erejéig 2 megoldás van (próbáld megtalálni őket, mielőtt megnézed az ábrákat!):
Ez a két gráf nem izomorf egymással, mert az első gráfban a két negyedfokú csúcs (3 és 4) össze van kötve egymással, a második gráfban viszont a negyedfokú csúcsok (2 és 4) nincsenek összekötve egymással. Egy másik lehetséges indoklás: az első gráfban van 3 hosszúságú kör (háromszög), de a másodikban nincs. Ennek a feladatnak izomorfia erejéig csak ez a két megoldása van. Ha a rajzaid nem úgy néznek ki, mint a fentiek, akkor az ábrákra kattintva megint át tudod másolni az éleket a CS Academy Graph Editor oldalára, és „Edit” módban rendezgetheted úgy a csúcsokat, hogy a saját ábráidat kapd. Ha több, mint két megoldást találtál, akkor biztosan lesznek közöttük izomorfak; ezt is ki tudod deríteni ezzel a módszerrel.
3. feladat. Adj meg olyan 5 csúcsú gráfokat (minél többet), amelyekben minden csúcs fokszáma 3.
Megoldás: Ilyen gráf nincs, mert egy ilyen gráfban a fokszámok összege 15 lenne. Márpedig a fokszámok összege minden gráfban páros szám, hiszen megegyezik az élek számának kétszeresével. (Ha ezt nem tudtad, akkor nem olvastad el az előadás anyagából amit kellett, és nem nézted meg a videókat sem!)
4. feladat. Adj meg olyan 6 csúcsú gráfokat (minél többet), amelyekben a csúcsok fokszámai a következők: 0,2,2,4,4,4.
Megoldás: Ilyen gráf sincs, de az indoklás egy kicsit bonyolultabb. A nulladfokú csúcs senkivel nincs összekötve (izolált pont), ezért gyakorlatilag az a kérdés, hogy van-e olyan 5 pontú gráf, amiben a fokszámok 2,2,4,4,4. Egy ilyen gráfban az élek száma 8 lenne (a fokszámok összegének fele). Ha 5 csúcsú teljes gráfunk lenne, akkor az élek száma 10 lenne. Tehát a mi gráfunk csak úgy készülhetne, hogy egy 5 csúcsú teljes gráfból elhagyunk 2 élt (és azután mellébiggyesztünk egy izolált csúcsot). Izomorfia erejéig két lehetőség van: a két elhagyott élnek vagy van közös végpontja, vagy nincs. Az alábbi ábrák mutatják ezt a két lehetőséget:
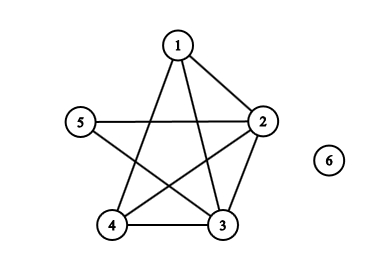
Az első esetben a fokszámsorozat 0,2,3,3,4,4, a második esetben pedig 0,3,3,3,3,4. Egyik esetben sem 0,2,2,4,4,4 jött ki a fokszámokra, a keresett gráf tehát nem létezik.
Megjegyzés: Ennek a feladatnak a tanulsága az, hogy attól, hogy a megadott számok összege páros, még nem biztos, hogy létezik olyan gráf, aminek pont ez a fokszámsorozata. A fokszámsorozatok teljes jellemzését (azaz szükséges és elégséges feltételt) az Erdős–Gallai-tétel adja meg. (Ha megengedünk hurokéleket és többszörös éleket is, akkor viszont minden páros összegű sorozathoz könnyen lehet konstruálni olyan gráfot, aminek pont az a fokszámsorozata – gondold meg, hogy miért!)
5. feladat. Adj meg olyan 6 csúcsú gráfokat (minél többet), amelyekben a csúcsok fokszámai a következők: 1,1,2,2,3,3.
Megoldás: Izomorfia erejéig 5 megoldás van (próbáld megtalálni őket, mielőtt megnézed az ábrákat!):
Akárcsak korábban, az ábrákra kattintva megkapod az élek felsorolását, és a CS Academy Graph Editor oldalán tudod állítgatni a gráfokat, hogy felismerd, a saját megoldásaid közül melyik melyikkel izomorf a fentiek közül.
Hasonló feladatokat találsz a feladatsorban (3.2–7. feladatok). Amikor a feladat azt mondja, hogy „a pontokat nem számozzuk meg”, az azt jelenti, hogy izomorfia erejéig számoljuk a megoldásokat (ahogy eddig is tettük). Amikor „megszámozzuk a pontokat”, akkor viszont különbözőnek tekintünk két izomorf gráfot, ha nem pont úgyanúgy vannak megszámozva (elnevezve) a csúcsaik (mint az 1. feladatban a második és a harmadik ábrán látható gráf). Így persze sokkal több lehetőség van, de ezzel most ne foglalkozzunk, elégedjünk meg a megoldások „számozás nélküli”, azaz izomorfia erejéig történő összeszámolásával.
 |
következő rész: Hamilton-út és Euler-vonal |