Határozzuk meg az
![]() határértéket, ha
a
határértéket, ha
a ![]() és
és ![]() valós paraméterekről tudjuk, hogy
valós paraméterekről tudjuk, hogy ![]() .
.
A ![]() kvóciensű
kvóciensű ![]() kezdő taggal rendelkező mértani sorozat összegképlete
kezdő taggal rendelkező mértani sorozat összegképlete
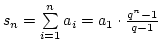 , ezt alkalmazva a számlálóban és a nevezőben is,
továbbá a
, ezt alkalmazva a számlálóban és a nevezőben is,
továbbá a
![]() nevezetes határértéket felhasználva kapjuk, hogy
nevezetes határértéket felhasználva kapjuk, hogy
![]() .
.