


Next: 7. Példa
Up: Sorozatok határértékének meghatározása I.
Previous: 5. Példa
Határozzuk meg az
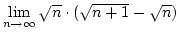 határértéket.
határértéket.
Ismét egy határozatlan kifejezéssel van dolgunk, újból az 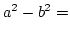
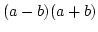 nevezetes azonosságot alkalmazva:
nevezetes azonosságot alkalmazva:
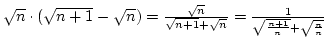 , ezért
, ezért
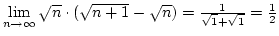 .
.
Róbert Vajda
2003-01-14
![]() határértéket.
határértéket.
![]()