


Next: Példa
Up: Határozott integrál
Previous: Különböző függvénygrafikonok által határolt
Határozzuk meg az 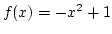 és a
és a 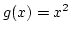 grafikonjai által határolt síktartomány területét.
grafikonjai által határolt síktartomány területét.
Megoldás: A két metszéspont koordinátája
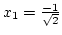 ,
,
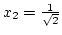 és
az
és
az 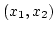 intervallumon
intervallumon 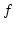 nagyobb mint
nagyobb mint 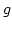 . Ezért
. Ezért
![$T=\int_{-1\over{\sqrt2}}^{1\over{\sqrt2}} (-x^2+1)-x^2 dx=
\left[-{2\over3}x^3+x\right]_{-1\over{\sqrt2}}^{1\over{\sqrt2}}={2\over3}\sqrt2$](img560.png) .
.
Róbert Vajda
2003-01-14
![$T=\int_{-1\over{\sqrt2}}^{1\over{\sqrt2}} (-x^2+1)-x^2 dx=
\left[-{2\over3}x^3+x\right]_{-1\over{\sqrt2}}^{1\over{\sqrt2}}={2\over3}\sqrt2$](img560.png) .
.
![]() ,
,
![]() és
az
és
az ![]() intervallumon
intervallumon ![]() nagyobb mint
nagyobb mint ![]() . Ezért
. Ezért
![$T=\int_{-1\over{\sqrt2}}^{1\over{\sqrt2}} (-x^2+1)-x^2 dx=
\left[-{2\over3}x^3+x\right]_{-1\over{\sqrt2}}^{1\over{\sqrt2}}={2\over3}\sqrt2$](img560.png) .
.