


Next: Megjegyzés
Up: Sorozatok határértékének meghatározása I.
Previous: 2. Példa
Határozzuk meg az
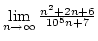 határértéket.
határértéket.
Mivel
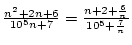 ,
a műveleti szabályokat alkalmazva kapjuk, hogy
,
a műveleti szabályokat alkalmazva kapjuk, hogy
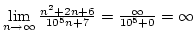
Róbert Vajda
2003-01-14
![]() határértéket.
határértéket.
![]() ,
a műveleti szabályokat alkalmazva kapjuk, hogy
,
a műveleti szabályokat alkalmazva kapjuk, hogy