


Next: Lemma
Up: Paricális deriváltak
Previous: 15. Példa
Az  pont az
pont az 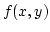 függvény lokális szélsőértékhelye, ha létezik egy olyan
függvény lokális szélsőértékhelye, ha létezik egy olyan 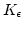 környezete
úgy, hogy
környezete
úgy, hogy
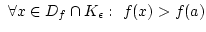 . Legyen
. Legyen 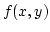 az
az 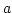 pont egy környezetében totálisan differenciálható.
Ekkor persze a parciális deriváltak is léteznek és ha
pont egy környezetében totálisan differenciálható.
Ekkor persze a parciális deriváltak is léteznek és ha 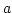 -ban lokális szélsőértékhely van, akkor lokális szélsőértéke
van az
-ban lokális szélsőértékhely van, akkor lokális szélsőértéke
van az
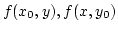 egyváltozós függvényeknek is, ezért a szélsőérték létezésének szükséges feltétele
, hogy
egyváltozós függvényeknek is, ezért a szélsőérték létezésének szükséges feltétele
, hogy
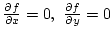 . Hogy ez még nem elégséges, arra jó
példa az
. Hogy ez még nem elégséges, arra jó
példa az
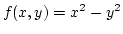 képlettel definiált un. nyeregfelület viselkedése az
képlettel definiált un. nyeregfelület viselkedése az 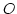 -ban.A következő lemmában
egy elégséges feltételt fogalmazunk meg.
-ban.A következő lemmában
egy elégséges feltételt fogalmazunk meg.
Róbert Vajda
2003-01-14