
Department Chair of Applied and Numerical Mathematics, University of Szeged
Scientific Director of
National Laboratory for Health Security, Hungary
Core
Group Leader of Computational Medicine, Hungarian Centre of
Excellence in Molecular Medicine
Alumni of Young Academy of Europe
Previous affiliations:


Research interests
Differential equations
Differential equations are the
mathematical descriptions of physical and biological systems that
continuously change in time. These equations are defined by
relationships between the current state of the system and the rate
of its change. Our goal is to predict the future behaviour of the
system, using analytic, qualitative or numerical investigations of
the solutions. 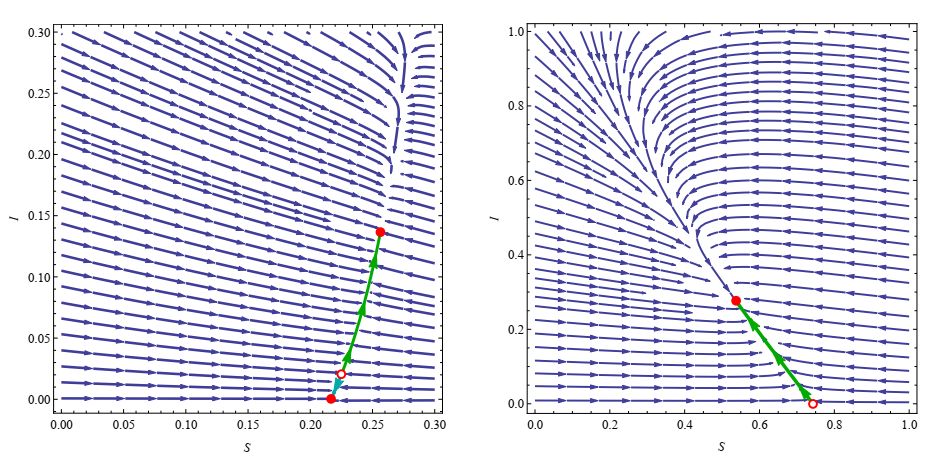
Mathematical epidemiology
Mathematical models can predict how infectious diseases progress to show the likely outcome of an epidemic. By disease modelling we can provide important information to public health by designing, evaluating and comparing different strategies to control the outbreak. The basic mathematical framework uses systems of differential equations called compartmental models.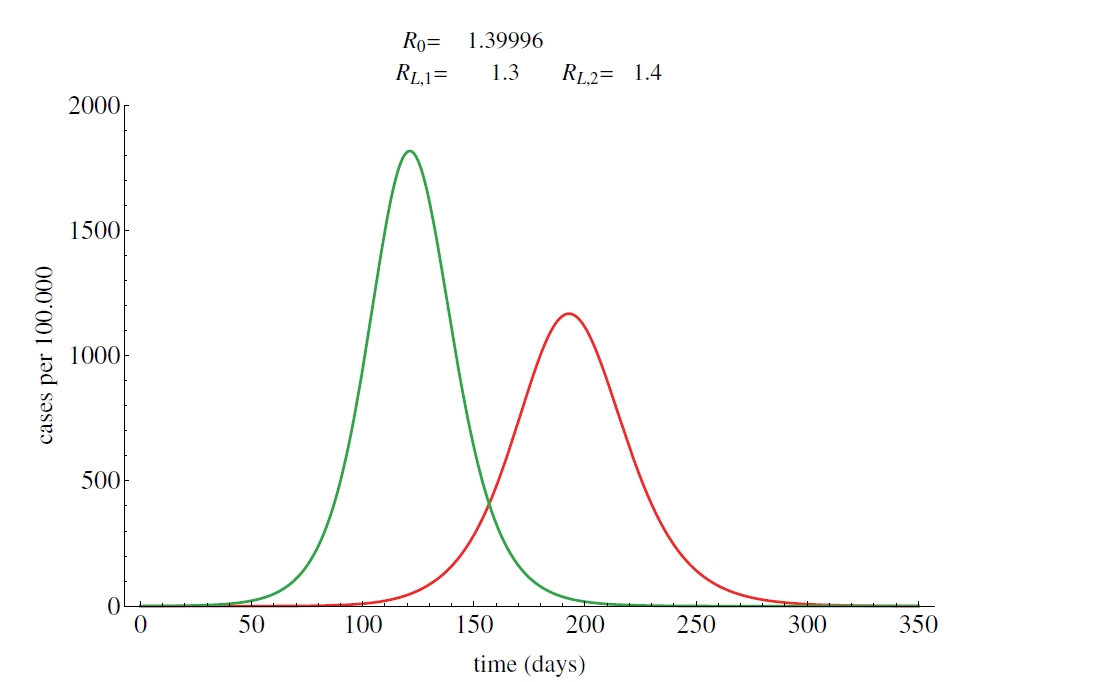
Nonlinear dynamics
Nonlinear dynamics describe the time evolution of systems where
the output is not proportional to the input. To understand complex
systems we need to take into account all the interactions of
variables and complicated feedbacks. A major goal is to describe
the geometric structure of attractors, that encapsulate the most
important information about the long term dynamics. 
Time delays
Time delays arise in various fields of engineering, physics and
biology. Dynamical systems including delays can be written as
delay differential equations (DDEs). Their right hand side is a
functional, and the corresponding phase space is infinite
dimensional. Nonlinear DDEs can show very interesting dynamics and
lead to fascinating and sophisticated mathematics.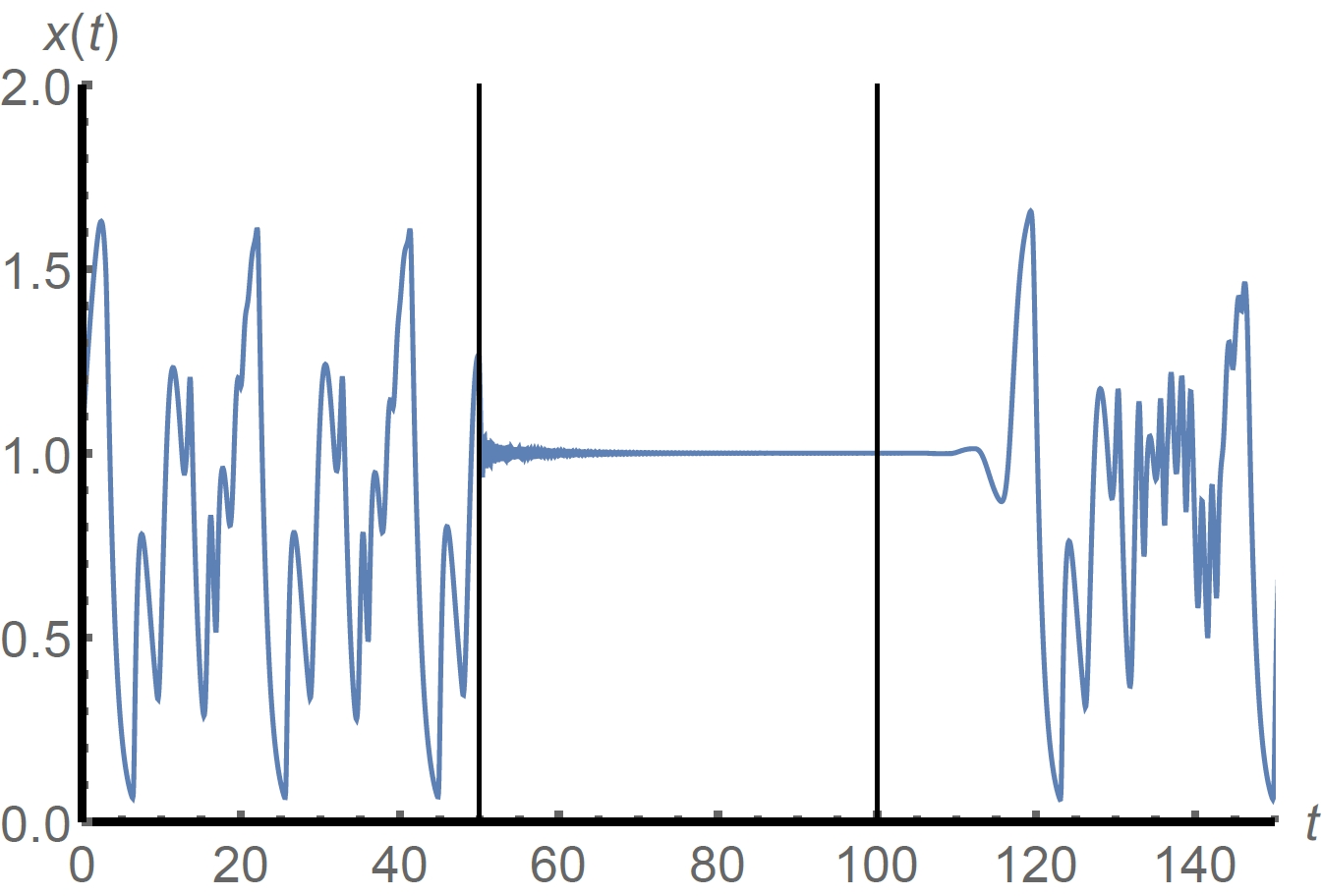
Modelling of cell biology processes
Cell proliferation, death and motility are key events in many
important cell biological processes, such as embryonic
development, tissue regeneration or the progression of cancer.
Mathematical models help to understand the collective behaviour
and the spatio-temporal dynamics of various cell populations,
which may lead to, for example, more efficient treatments of
cancer.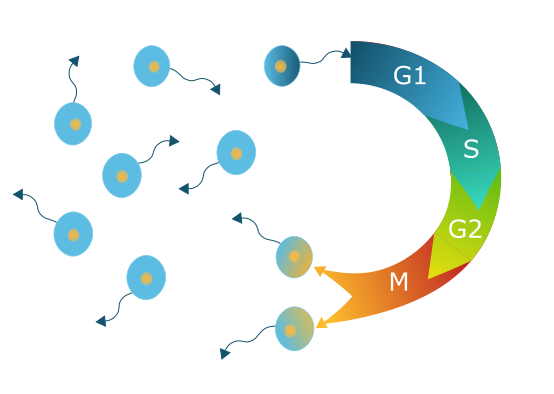
Bifurcation theory
Bifurcations represent situations when the behaviour of a system
suddenly changes as a parameter is crossing a critical value. They
are associated to loss of stability, the appearance or destruction
of equilibria, sudden emergence of periodic or more complex
behaviours. The birth of chaos from simple dynamics can be
understood through a cascade of subsequent bifurcations.
Research Projects
| Time | Title | Funded by | Role |
|---|---|---|---|
| 2025 - 2028 | RAPID-GRIP (Szeged-Yale-Kyoto) | 2024-1.2.3-HU-RIZONT-2024-00034 | PI |
| 2025 - 2027 | Genomic Epidemiology | HUNREN-TKCS-2024 | co-PI |
| 2022 - 2026 | National Laboratory for Health Security | RRF-2.3.1-21-2022-00006, NKFIH, National Laboratory Programs, | PI |
| 2022 - 2024 | European partnership for Pandemic Preparedness | BE READY, EU HORIZON-HLTH-2021-DISEASE-04 No. 101057795 | part. |
| 2020 - 2023 | CoMix in EPIPOSE | EU SOCIETAL CHALLENGES No. 101003688 | part. |
| 2022 - 2023 | In-host and pharmacological dynamics of SARS-CoV-2 infection | 2019-2.1.11-TÉT-2020-00231 Hungary-Serbia Bilateral Project (with D. Selesi, Novi Sad) | co-PI |
| 2021 - 2025 | EVOGAMESPLUS European Training Network | EU EXCELLENT SCIENCE - Marie Skłodowska-Curie Actions, No. 955708 | sup. |
| 2020 - 2022 | Modelling, analysis, and predictions for COVID-19 in Hungary | NKFIH COVID Fund 2020-2.1.1-ED-2020-00003 | PI |
| 2019 - 2025 | Nonlinear Dynamics in the Mathematical Models of Cell Biology | Frontline (Élvonal), National Research, Development and Innovation Office NKFI | PI |
| 2017 - 2019 | TEMPOMATH | EU Marie Sklodowska-Curie Individual Fellowship No. 748193 | PI |
| 2011 - 2016 | EPIDELAY | European Research Council Starting Investigator Grant No. 259559 | PI |
| 2017 - 2019 | Dynamics and Control of Metapopulations | National Research, Development and Innovation Office NKFI KH 125628 | PI |
| 2017 - 2021 | Functional Differential Equations in Mathematical Epidemiology | National Research, Development and Innovation Office NKFI FK 124016 | PI |
| 2018 - 2019 | Applications of Dynamical Systems in Population Biology | TET16JP Hungary-Japan Bilateral Project (with H. Inaba, Tokyo, JSPS) | co-PI |
| 2012 - 2013 |
REFADE - Cross-Border Research on Functional Analysis and Differential Equations | Hungary-Romania Cross-Border Co-operation Programme 2007-2013
(with A. Popovici, Timisoara) |
co-PI |





