Next: 6. Feladat
Up: Teljes függvénydiszkusszió
Previous: 4. Feladat
Végezzünk teljes függvénydiszkussziót, ha
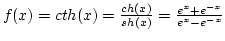 .
.
-
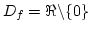 , zérushelyek: mivel
, zérushelyek: mivel 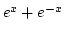 mindig pozitív, nincs zéróhely,
mindig pozitív, nincs zéróhely,
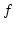 páratlan
páratlan
-
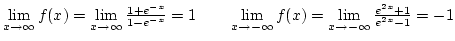

-
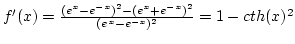 ,
, 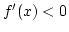 , nincs zéróhely
, nincs zéróhely
-
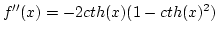 ,
, 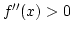 , ha
, ha 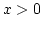 , ill.
, ill. 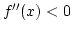 , ha
, ha 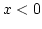 , nincs zéróhely
, nincs zéróhely
- Táblázat:
Róbert Vajda
2003-01-14