1. Feladat

Bizonyítsuk be teljes indukcióval, hogy

$1^2+2^2+3^2+\dots+n^2={n(n+1)(2n+1)\over6}.$

Megoldás: $n=1$esetén ${1(1+1)(2\cdot1+1)\over6}={2\cdot3\over6}=1$

Tegyük fel, hogy n-re már igaz az állítás. Vizsgáljuk (n+1)-re:

$1^2+2^2+\dots+n^2+(n+1)^2=(1^2+2^2+\dots+n^2)+(n+1)^2\matrix{(IF.)\cr=\cr }$

${n(n+1)(2n+1)\over6}+(n+1)^2={(n+1)[n(2n+1)+6(n+1)]\over6} ={(n+1)(2n^2+7n+6)\over6}=$

${(n+1)(n+2)(2n+3)\over6}={(n+1)((n+1)+1)(2(n+1)+1)\over6},$

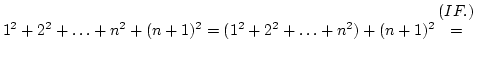
s mivel a bizonyítandó képletet kaptuk "$n$ helyett $(n+1)$-re",

a teljes indukciós bizonyítást befejeztük.