


Next: Megjegyés
Up: Integrálás helyettesítéssel
Previous: Integrálás helyettesítéssel
Ha 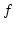 egy primitív függvénye
egy primitív függvénye 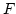 , akkor
, akkor
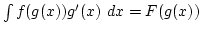 ,
amit formálisan úgy alkalmazhatunk, hogy
,
amit formálisan úgy alkalmazhatunk, hogy 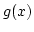 helyébe egy új
változót, mondjuk
helyébe egy új
változót, mondjuk 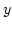 -t helyettesítünk,
-t helyettesítünk, 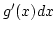 helyébe pedig
helyébe pedig 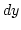 -t, azaz:
-t, azaz:
Róbert Vajda
2003-01-14