


Next: Lemma
Up: Paricális deriváltak
Previous: Megjegyzés
Emlékeztető. Ha 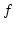 deriválható
deriválható 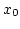 -ban, akkor érvényes a függvényértékkülönbségre az alábbi képlet:
-ban, akkor érvényes a függvényértékkülönbségre az alábbi képlet:
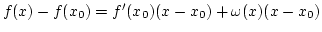 , ahol
, ahol
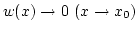 .
Az
.
Az 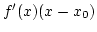 kifejezés lineáris, és a formula azt mutatja, hogy
kifejezés lineáris, és a formula azt mutatja, hogy 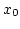 kis környezetében ez a lineáris közelítés jó.
Ennek általánosításaként azt mondjuk, hogy az
kis környezetében ez a lineáris közelítés jó.
Ennek általánosításaként azt mondjuk, hogy az 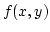 totálisan differenciálható a
totálisan differenciálható a 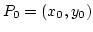 pontban, ha
vannak olyan
pontban, ha
vannak olyan 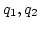 állandók, hogy
állandók, hogy 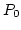 egy környezetében érvényes az
egy környezetében érvényes az
 előállítás.
előállítás.
Róbert Vajda
2003-01-14