Példa.
![]() s a fokszám a számlálóban kisebb
s a fokszám a számlálóban kisebb
![]()
ahol a faktorok irreducibilisek.
A parciális törtek ![]() esetén
esetén
![]()
A parciális törtek ![]() esetén
esetén
![]()
Az eljárás sikere azon múlik, hogy ez mindig megtehető.
4a. Lineáris faktorokhoz tartozó parciális törtek integrálása
![]()
![]()
4b. Másodfokú irred. faktorokhoz tartozó parciális törtek integrálása
![]()
![]()
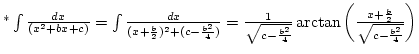
![]() Szétszedjük lineáris számlálójú
Szétszedjük lineáris számlálójú ![]() és konstans számlálójú törtre. Az elsőt helyettesítéssel, a másodikat rekurzióval intézzük el.
és konstans számlálójú törtre. Az elsőt helyettesítéssel, a másodikat rekurzióval intézzük el.
![]()
![]()
![]()
![]()
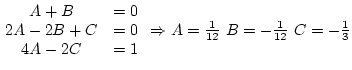
![]()
![]()
![]()