Subsections
Legyen 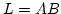 irányított egyszerű görbe egy beosztása
irányított egyszerű görbe egy beosztása
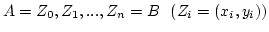 és legyen
és legyen
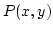 és
és 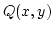 L-en értelmezett,
L-en értelmezett, 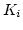 a
a 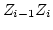 ív tetsző leges pontja. Képezzük a következő közelítő összeget:
ív tetsző leges pontja. Képezzük a következő közelítő összeget:
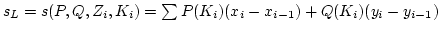 . Ha ez a beosztás minden határon túli finomítása esetén
tart egy értékhez, akkor ezt a
. Ha ez a beosztás minden határon túli finomítása esetén
tart egy értékhez, akkor ezt a 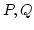 függvények
függvények 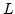 menti integráljának nevezzük.
menti integráljának nevezzük.
1. Hasonló műveleti szabályok érvényesek mint a közönséges integrál esetén.
2. Ha nem egyszerű a görbe, akkor megpróbáljuk ilyenekből összetenni, s a szakaszokon a vonalintegrál már értelmezett, így
az összetett görbén a vonalintegrál a szakaszokon vett integrálok összege.
3. Nem definició szerint számolunk, hanem visszavezetjük a vonalintegrál kiszámítását
közönséges integrálok meghatározására.
4. Nevezetes probléma annak eldöntése, milyen szükséges és elegendő feltétellt lehet adni
az integrál úttól való függetlenségére.
5. Alkalmazás. Munkavégzés (speciálisan konzervatív erőterekben): A vonalintegrál
fizikailag interpretálható úgy, mint egy változó
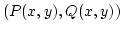 erő egy
erő egy 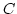 integrációs
út (görbe) mentén végzett munkája.
6. 3 változós függvények esetén is értelmezhető vonalintegrál.
integrációs
út (görbe) mentén végzett munkája.
6. 3 változós függvények esetén is értelmezhető vonalintegrál.
Tegyük fel, hogy
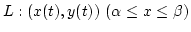 egyszerű és síma
egyszerű és síma 
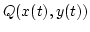 pedig folytonosak a paramétertartományon. Ekkor:
pedig folytonosak a paramétertartományon. Ekkor:

Határozzuk meg a következő vonalintegrált, ahol 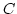 a standard ellipszis felső része,
negatív irányban bejárva:
a standard ellipszis felső része,
negatív irányban bejárva:
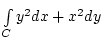 .
Megoldás.
.
Megoldás.
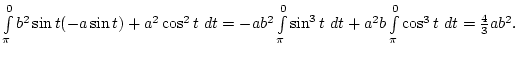
Egy mezőt a konstans nagyságú, az x-tengely pozitív fele által kijelölt irányú 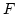 erő generál.
Határozzuk meg a mező által végzett munkát, ha egy pont az
erő generál.
Határozzuk meg a mező által végzett munkát, ha egy pont az 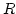 sugarú, origó centrumú negyedkörön halad végig
az első síknegyedben, az óra járásával megegyező irányban.
sugarú, origó centrumú negyedkörön halad végig
az első síknegyedben, az óra járásával megegyező irányban.
Megoldás.
![$P(x,y)=F, Q(x,y)=0\Rightarrow F_f=\int\limits_{\pi\over2}^0 -FR\sin t dt
=FR[\cos t]_{\pi\over2}^0=FR$](img189.png) .
.
Róbert Vajda
2003-04-23


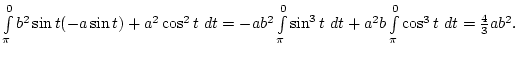
![$P(x,y)=F, Q(x,y)=0\Rightarrow F_f=\int\limits_{\pi\over2}^0 -FR\sin t dt
=FR[\cos t]_{\pi\over2}^0=FR$](img189.png) .
.