Subsections
A második alapfeladat: Határozzuk meg egy 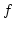 függvény grafikonja alatti területet, azaz egy kicsit pontosabban:
határozzuk meg az
függvény grafikonja alatti területet, azaz egy kicsit pontosabban:
határozzuk meg az 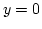 ,
, 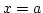 ,
, 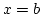 egyenletű egyenesek és a nemnegatív
egyenletű egyenesek és a nemnegatív 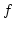 függvény grafikonja által határolt síktartomány
(görbevonalú trapéz) területét.
függvény grafikonja által határolt síktartomány
(görbevonalú trapéz) területét.
Megoldás: Ha 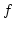 integrálható
integrálható ![$[a,b]$](img95.png) -n, akkor
-n, akkor
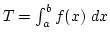 .
.
Newton-Leibniz formula, Ha 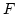 az
az 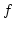 egy primitív függvénye, akkor
egy primitív függvénye, akkor
![$\int_a^b f(x) dx=\left[F(x)\right]_a^b=F(b)-F(a).$](img97.png)
Határozzuk meg az 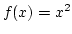 képlettel adott függvény grafikonja alatti területet, ha
képlettel adott függvény grafikonja alatti területet, ha 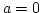 és
és 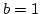 .
.
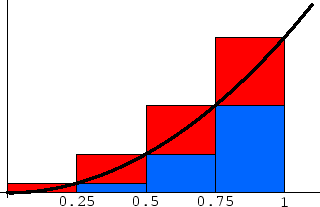
Megoldás:
![$T=\int_a^b f(x) dx=\int_0^1 x^2 dx=\left[{x^3\over3}\right]_0^1={1\over3}$](img102.png) .
.
Ha az előző problémafelvetésben a 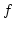 -re vonatkozó nemnegativitási feltételt elhagyjuk, akkor a határozzott
integrál értéke előjeles területet ad, vagyis pl.
-re vonatkozó nemnegativitási feltételt elhagyjuk, akkor a határozzott
integrál értéke előjeles területet ad, vagyis pl.
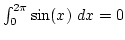 , jóllehet a keltkező síktartomány
területe nyilván nem
, jóllehet a keltkező síktartomány
területe nyilván nem 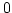 , hanem
, hanem 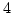 .
.
Ha 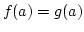 és
és 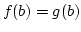 , továbbá
, továbbá
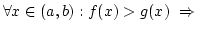 a 2 függvénygrafikon által határolt terület
a 2 függvénygrafikon által határolt terület
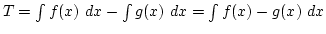 . Ezért a következő lépéseket kell elvégeznük:
. Ezért a következő lépéseket kell elvégeznük:
- Metszéspontok koordinátáinak meghatározása
- Meg kell állapítanunk, hogy az
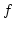 vagy a
vagy a 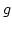 nagyobb. Tegyük fel, hogy az
nagyobb. Tegyük fel, hogy az 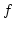 bizonyult nagyobbnak
bizonyult nagyobbnak
- Meghatározzuk az
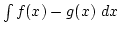 értéket.
értéket.
Határozzuk meg az 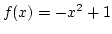 és a
és a 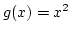 grafikonjai által határolt síktartomány területét.
grafikonjai által határolt síktartomány területét.
Megoldás: A két metszéspont koordinátája
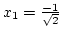 ,
,
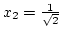 és
az
és
az 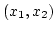 intervallumon
intervallumon 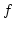 nagyobb mint
nagyobb mint 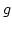 . Ezért
. Ezért
![$T=\int_{-1\over{\sqrt2}}^{1\over{\sqrt2}} (-x^2+1)-x^2 dx=
\left[-{2\over3}x^3+x\right]_{-1\over{\sqrt2}}^{1\over{\sqrt2}}={2\over3}\sqrt2$](img116.png) .
.
Határozzuk meg az
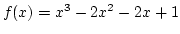 és a
és a 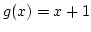 grafikonjai által határolt síktartomány területét.
grafikonjai által határolt síktartomány területét.
Megoldás: A metszéspontok x-koordinátái 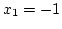 ,
, 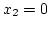 , és
, és 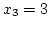 ,
az
,
az 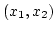 intervallumon
intervallumon 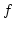 nagyobb mint
nagyobb mint 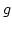 , az
, az 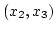 intervallumon viszont
intervallumon viszont 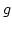 nagyobb mint
nagyobb mint 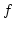 . Ezért
. Ezért
![$T=\int_{-1}^0 (x^3-2x^2-2x+1)-(x+1) dx-
\int_0^3 (x+1)-(x^3-2x^2-2x+1) dx=
...
...over4}x^4+{2\over3}x^3+{3\over2}x^2\right]_0^3={7\over12}+{45\over4}={71\over6}$](img123.png) .
.
A helyettesítés ugyanúgy történik mint a primitív függvény keresésénél. csak most a határok is megváltoznak. Ezért
![$\int_a^b f(g(x))g'(x) dx=\int_{g(a)}^{g(b)} f(y)dy=\left[F(y)\right]_{g(a)}^{g(b)}$](img124.png) .
.
Határozzuk meg az egység sugarú (negyed-)kör területét.
Megoldás: Az origó középpontú 1 sugarú kör egyenlete : 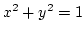 , ezért az első síknegyedet választva
az explicit függvénykapcsolatot az
, ezért az első síknegyedet választva
az explicit függvénykapcsolatot az
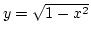 képlet írja le. A meghatározandó integrál tehát:
képlet írja le. A meghatározandó integrál tehát:
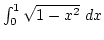 . Alkalmazzuk a
. Alkalmazzuk a 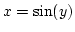 helyettesítést.
helyettesítést.
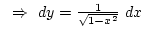
![$\int_0^1 \sqrt{1-x^2} dx=\int_0^{\pi\over2} 1-\sin^2(y) dy=\int_0^{\pi\over2} \...
...\cos(2y) dy={1\over2}\left[y+{\sin(2y)\over2}\right]_0^{\pi\over2}={\pi\over4}$](img130.png) .
.
Ezért az egészkörnek a területe 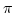 , és a hasonlóság miatt az R sugarú kör területe
, és a hasonlóság miatt az R sugarú kör területe
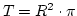 .
.
2. Megoldás. Ha ismerjük a polárkoordinátákra vonatkozó területképletetet, akkor gyorsabban
célhoz érünk:
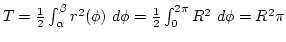 .
.
Egy test gyorsulása a '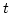 '-edik másodpercben:
'-edik másodpercben:
![$a(t)=3\sin(2t) [{m\over{s^2}}]$](img135.png) , továbbá tudjuk,
hogy
, továbbá tudjuk,
hogy 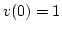 és
és
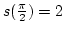 . Mennyi utat tesz meg '
. Mennyi utat tesz meg '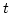 ' másodperc elteltével? Mennyi az átlagsebessége
a
' másodperc elteltével? Mennyi az átlagsebessége
a 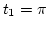 és a
és a 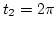 közötti időintervallumban?
közötti időintervallumban?
Megoldás:
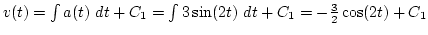 , és mivel
, és mivel 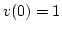 , így
, így
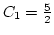 .
.
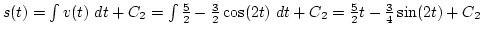 , és mivel
, és mivel
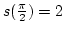 , így
, így
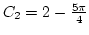 .
.
Határozzuk meg az 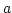 és
és 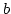 paraméterű ellipszis területét.
paraméterű ellipszis területét.
Megoldás: Az ellipszis paraméteres előállítása és a paraméteres
előállításban megadott görbe által határolt síktaromány területe:
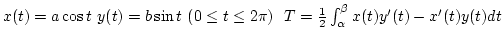 .
.
Ezért:
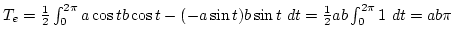 .
.
Határozzuk meg az 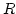 sugarú kör kerületét.
sugarú kör kerületét.
Megoldás: Az origó középpontú 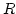 sugarú felső félkör egyenlete és a ívhossz
képlete:
sugarú felső félkör egyenlete és a ívhossz
képlete:
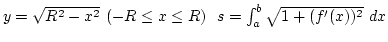
Ezért:
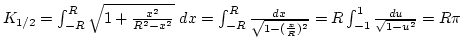 .
.
2. Megoldás: A paraméteres megadás szerint számolva
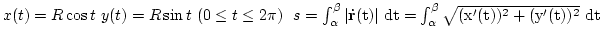
Ezért:
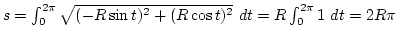 .
.
Határozzuk meg az 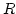 sugarú és
sugarú és 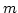 magasságú egyenes körkúp térfogatát.
magasságú egyenes körkúp térfogatát.
Megoldás: Az egyenes körkúpot forgástestként tekinthetjük, ha az
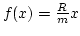 egyenest
egyenest
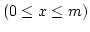 megforgatjuk az
megforgatjuk az 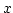 tengely körül.
tengely körül.
Ezért:
![$V=\pi\int_a^b f^2(x) dx=\pi\int_0^m{R^2\over m^2}x^2 dx=
\pi{R^2\over m^2}[{x^3\over3}]_0^m={\pi R^2m\over3}$](img157.png) .
.
Határozzuk meg az 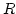 sugarú gömb térfogatát.
sugarú gömb térfogatát.
Megoldás: Az
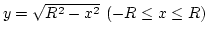 egyenletű görbét megfogatva az
egyenletű görbét megfogatva az 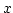 tengely
körül:
tengely
körül:
![$V=\pi\int_{-R}^R R^2-x^2 dx=\pi[R^2x-{x^3\over3}]_{-R}^R={4\over3}\pi R^3$](img159.png) .
.
Róbert Vajda
2003-04-23
![]() integrálható
integrálható ![]() -n, akkor
-n, akkor
![]() .
.

![$T=\int_a^b f(x) dx=\int_0^1 x^2 dx=\left[{x^3\over3}\right]_0^1={1\over3}$](img102.png) .
.
![]() ,
,
![]() és
az
és
az ![]() intervallumon
intervallumon ![]() nagyobb mint
nagyobb mint ![]() . Ezért
. Ezért
![$T=\int_{-1\over{\sqrt2}}^{1\over{\sqrt2}} (-x^2+1)-x^2 dx=
\left[-{2\over3}x^3+x\right]_{-1\over{\sqrt2}}^{1\over{\sqrt2}}={2\over3}\sqrt2$](img116.png) .
.
![]() ,
, ![]() , és
, és ![]() ,
az
,
az ![]() intervallumon
intervallumon ![]() nagyobb mint
nagyobb mint ![]() , az
, az ![]() intervallumon viszont
intervallumon viszont ![]() nagyobb mint
nagyobb mint ![]() . Ezért
. Ezért
![]() .
.
![$\int_0^1 \sqrt{1-x^2} dx=\int_0^{\pi\over2} 1-\sin^2(y) dy=\int_0^{\pi\over2} \...
...\cos(2y) dy={1\over2}\left[y+{\sin(2y)\over2}\right]_0^{\pi\over2}={\pi\over4}$](img130.png) .
.
![]() , és a hasonlóság miatt az R sugarú kör területe
, és a hasonlóság miatt az R sugarú kör területe
![]() .
.
![]() .
.
![]() , és mivel
, és mivel ![]() , így
, így
![]() .
.
![]() , és mivel
, és mivel
![]() , így
, így
![]() .
.
![]() .
.
![]() .
.
![]() sugarú felső félkör egyenlete és a ívhossz
képlete:
sugarú felső félkör egyenlete és a ívhossz
képlete:
![]()
![]() .
.
![]()
![]() .
.
![]() egyenest
egyenest
![]() megforgatjuk az
megforgatjuk az ![]() tengely körül.
tengely körül.
![]() .
.
![]() egyenletű görbét megfogatva az
egyenletű görbét megfogatva az ![]() tengely
körül:
tengely
körül:
![]() .
.