Subsections
Ha 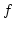 egy primitív függvénye
egy primitív függvénye 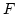 , akkor
, akkor
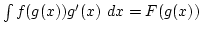 ,
amit formálisan úgy alkalmazhatunk, hogy
,
amit formálisan úgy alkalmazhatunk, hogy 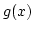 helyébe egy új
változót, mondjuk
helyébe egy új
változót, mondjuk 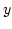 -t helyettesítünk,
-t helyettesítünk, 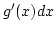 helyébe pedig
helyébe pedig 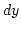 -t, azaz:
-t, azaz:
Tulajdonképpen már az egyik előző feladatmegoldásnál is burkoltan ezt a módszert alkalmaztuk, hiszen
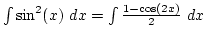 , és itt
, és itt 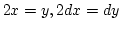 helyettesítés miatt
helyettesítés miatt
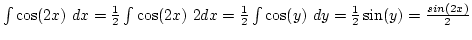
Ha ezt a módszert szeretnénk alkalmazni, először meg kell próbálnunk leválasztani a 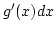 kifejezést:
kifejezést:
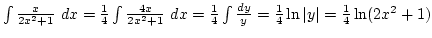
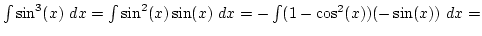
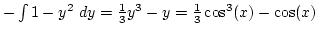
Róbert Vajda
2003-04-23
![]() , és itt
, és itt ![]() helyettesítés miatt
helyettesítés miatt
![]()
![]()