Markov-láncok

Időjárás-előrejelzés

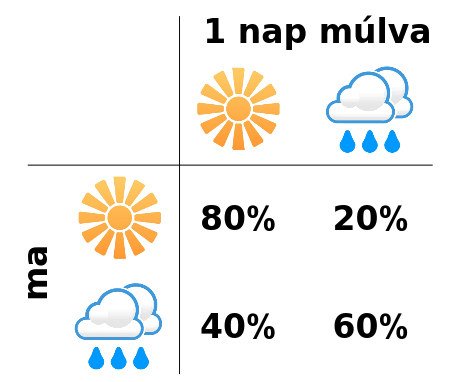
Tfh. kétféle időjárás van: jó idő és rossz idő, és ezek a következő egyszerű szabály szerint változnak:

Ha ma jó idő van, 80% eséllyel holnap is az lesz, és 20% valószínűséggel elromlik holnapra az idő.
Ha ma rossz idő van, 60% eséllyel holnap is az lesz, és 40% valószínűséggel megjavul holnapra az idő.

Milyen idő lesz 1, 2, 3,… nap múlva?

%display latex
P = matrix(QQ, [[0.8,0.2], [0.4,0.6]])
k=1
pretty_print(LatexExpr("P^{%.0f}="%(k)),n(P^k,digits=4))

Határozzuk meg a $P$ átmenetmátrix karakterisztikus polinomját és sajátértékeit:

E = matrix(QQ, [[1,0], [0,1]])
karpol = (P-x*E).det().expand()
pretty_print(karpol); pretty_print(" ")
gyokok = karpol.roots()
pretty_print(gyokok); pretty_print(" ")
lambda_1 = gyokok[0][0]
pretty_print(LatexExpr("\\lambda_1="),lambda_1); pretty_print(" ")
lambda_2 = gyokok[1][0]
pretty_print(LatexExpr("\\lambda_2="),lambda_2)

Határozzuk meg a $\lambda_1$ sajátértékhez tartozó sajátalteret:

pretty_print(LatexExpr("(P-\\lambda_1 E)^T ="),(P-lambda_1*E).transpose(),LatexExpr("\\rightsquigarrow"),(P-lambda_1*E).transpose().rref())

A sajátaltér egydimenziós, egy bázisvektora például:

v_1 = (P-lambda_1*E).transpose().rref().columns()[-1]*(-1)+vector([0,1])
pretty_print(LatexExpr("\\mathbf{v}_1="),v_1);

Határozzuk meg a $\lambda_2$ sajátértékhez tartozó sajátalteret is:

pretty_print(LatexExpr("(P-\\lambda_2 E)^T ="),(P-lambda_2*E).transpose(),LatexExpr("\\rightsquigarrow"),(P-lambda_2*E).transpose().rref())

Ez a sajátaltér is egydimenziós, egy bázisvektora például:

v_2 = (P-lambda_2*E).transpose().rref().columns()[-1]*(-1)+vector([0,1])
pretty_print(LatexExpr("\\mathbf{v}_2="),v_2);

Diagonalizáljuk a $P$ mátrixot:

#A sajátbázisról a standard bázisra való áttérés mátrixa:
Q = matrix(QQ, [v_1, v_2])
#A sajátbázisbeli mátrix:
D = Q*P*Q^(-1)
pretty_print(LatexExpr("Q="),Q,LatexExpr("\\quad Q^{-1}="),Q^(-1)); pretty_print(" ")
pretty_print(LatexExpr("D=QPQ^{-1}="),D)

Ellenőrzés (visszakapjuk-e a $P$ mátrixot?):

pretty_print(LatexExpr("Q^{-1}DQ="),Q,LatexExpr("\\begin{pmatrix} \\lambda_1 & 0 \\\\ 0 & \\lambda_2 \\end{pmatrix}"),Q^(-1),LatexExpr("="));
pretty_print(LatexExpr("="),n(Q^(-1)*D*Q,digits=4)); pretty_print(" ")
pretty_print(LatexExpr("P="),n(P,digits=4))

Ellenőrzés (visszakapjuk-e a $P^{5}$ mátrixot?):

pretty_print(LatexExpr("Q^{-1}D^{5}Q="),Q,LatexExpr("\\begin{pmatrix} \\lambda_1^{5} & 0 \\\\ 0 & \\lambda_2^{5} \\end{pmatrix}"),Q^(-1),LatexExpr("=")); pretty_print(" ")
pretty_print(LatexExpr("="),Q,n(D^5,digits=4),Q^(-1),LatexExpr("=")); pretty_print(" ")
pretty_print(LatexExpr("="),n(Q^(-1)*D^5*Q,digits=4)); pretty_print(" ")
pretty_print(LatexExpr("P^{5}="),n(P^5,digits=4))

Ezzel a formulával a $P^{5}$ mátrixot (sőt, általánosan a $P^n$ mátrixot is) könnyen ki lehet számítani kézzel is.

Markov-láncok

Tfh. egy rendszer (pl. időjárás) $n$-féle állapotban lehet, és ha most éppen az $i$-edik állapotban van, akkor $p_{ij}$ valószínűséggel kerül a $j$-edik állapotba a következő lépésben. Az ilyen rendszert (diszkrét idejű, véges, homogén) Markov-láncnak nevezzük.

Legyen $P$ az átmenet-valószínűségek mátrixa: $$P = \begin{pmatrix} p_{11} & \dots & p_{1n} \\ \vdots & \ddots & \vdots \\ p_{n1} & \dots & p_{nn} \end{pmatrix} \in \mathbb{R}^n.$$ Ekkor $P^k$ írja le a $k$-lépéses átmenet-valószínűségeket. A $P$ mátrix úgynevezett sztochasztikus mátrix:

$0 \leq p_{ij} \leq 1$;
$p_{i1}+\dots+p_{in}=1$ (minden sorösszeg $1$).

Az utóbbiból következik, hogy

$P\mathbb{1}=\mathbb{1}$, ahol $\mathbb{1}$ a csupa egyesből álló (oszlop)vektor,
azaz $\mathbb{1}$ jobb oldali sajátvektor $\lambda=1$ sajátértékkel, és így $1$ gyöke a karakterisztikus polinomnak.
Ekkor létezik a $\lambda=1$ sajátértékhez bal oldali sajátvektor is: $\mathbf{v}P=\mathbf{v}$.

Perron–Frobenius-tétel (sztochasztikus mátrixokra):

Ha $P \in \mathbb{R}^{n \times n}$ csupa pozitív számból álló sztochasztikus mátrix, akkor

a $\lambda=1$ sajátérték algebrai multiplicitása $1$ (és így a geometriai is $1$);
minden más (komplex) sajátérték abszolút értéke kisebb $1$-nél;
van olyan $\lambda=1$ sajátértékhez tartozó bal oldali sajátvektor, amelynek minden eleme pozitív.

A $\lambda=1$ sajátértékhez tartozó bal oldali $\mathbf{s}=(q_1,\dots,q_n)$ sajátvektort választhatjuk úgy, hogy $$0 \lt q_i \lt 1, \qquad q_1+\dots+q_n=1$$ teljesüljön. Ekkor $\mathbf{s}=(q_1,\dots,q_n)$ egy valószínűségi eloszlás, amit stacionárius eloszlásnak nevezünk. A $\lim_{k\to\infty}P^k$ mátrix minden sorában az $\mathbf{s}$ vektor van.

A fenti időjárás-előrejelzős példában a $\lambda=1$-hez megtalált sajátvektort kell „normálni”, hogy megkapjuk a stacionárius eloszlást:

v=(P-E).transpose().rref().columns()[-1]*(-1)+vector([0,1])
pretty_print(LatexExpr("\\mathbf{v}="),v); pretty_print(" ")
s=1/sum(v)*v
pretty_print(LatexExpr("\\mathbf{s}="),s)

Peti áll a ház előtt…

Írjuk fel az átmenet-valószínűségek mátrixát:

%display latex
P = matrix(QQ, [[0,1,0], [0.8,0,0.2],[0,1,0]])
pretty_print(LatexExpr("P="),n(P,digits=2))

Határozzuk meg a $P$ mátrix karakterisztikus polinomját és sajátértékeit:

E = matrix(QQ, [[1,0,0], [0,1,0], [0,0,1]])
karpol = (P-x*E).det().expand()
pretty_print(karpol); pretty_print(" ")
gyokok = karpol.roots()
pretty_print(gyokok); pretty_print(" ")
lambda_1 = gyokok[0][0]
pretty_print(LatexExpr("\\lambda_1="),lambda_1); pretty_print(" ")
lambda_2 = gyokok[1][0]
pretty_print(LatexExpr("\\lambda_2="),lambda_2); pretty_print(" ")
lambda_3 = gyokok[2][0]
pretty_print(LatexExpr("\\lambda_3="),lambda_3)

Határozzuk meg a $\lambda=1$ sajátértékhez tartozó sajátalteret:

pretty_print(LatexExpr("(P-E)^T ="),n((P-E).transpose(),digits=2),LatexExpr("\\rightsquigarrow"),n((P-E).transpose().rref(),digits=2))

A sajátaltér egydimenziós, egy bázisvektora például:

v_1 = (P-E).transpose().rref().columns()[-1]*(-1)+vector([0,0,1])
pretty_print(LatexExpr("\\mathbf{v}_1="),n(v_1,digits=2));

Határozzuk meg a stacionárius eloszlást:

s=1/sum(v_1)*v_1
pretty_print(LatexExpr("\\mathbf{s}="),n(s,digits=2))

Hol lesz Peti 100 óra múlva?

pretty_print(LatexExpr("P^{100}="),n(P^100,digits=2))

Mi történik Petivel???

for k in range(1,6):
	pretty_print(LatexExpr("P^{%.0f}="%(k)),n(P^k,digits=2))
	pretty_print(" ")

Szörfözés a neten

Tfh. az internet csak 5 weboldalból áll:

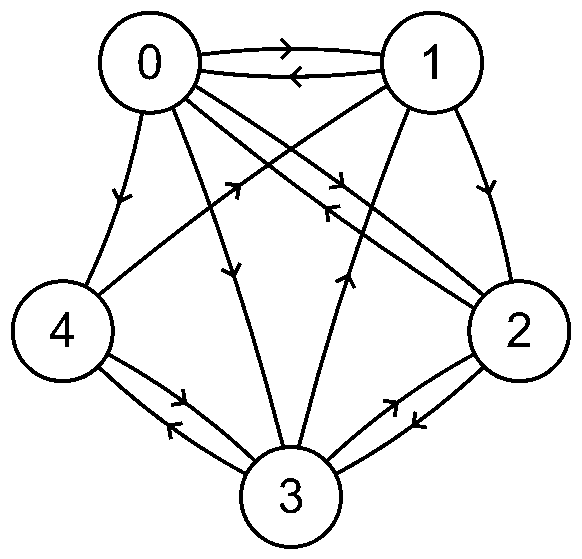
Egy tetszőleges oldalról indulunk, és véletlenszerűen klikkelünk a linkekre. Hosszú távon az időnk mekkora hányadát töltjük az egyes oldalakon?

Írjuk fel az átmenet-valószínűségek mátrixát:

%display latex
P = matrix(QQ, [[0,1/4,1/4,1/4,1/4], [1/2,0,1/2,0,0], [1/2,0,0,1/2,0], [0,1/3,1/3,0,1/3], [0,1/2,0,1/2,0]])
pretty_print(LatexExpr("P="),n(P,digits=2))

Határozzuk meg a $\lambda=1$ sajátértékhez tartozó sajátalteret:

E = matrix(QQ, [[1,0,0,0,0], [0,1,0,0,0], [0,0,1,0,0],[0,0,0,1,0],[0,0,0,0,1]])
pretty_print(LatexExpr("(P-E)^T ="),n((P-E).transpose(),digits=2),LatexExpr("\\rightsquigarrow"),n((P-E).transpose().rref(),digits=4))

A sajátaltér egydimenziós, egy bázisvektora például:

v_1 = (P-E).transpose().rref().columns()[-1]*(-1)+vector([0,0,0,0,1])
pretty_print(LatexExpr("\\mathbf{v}_1="),n(v_1,digits=4));

Határozzuk meg a stacionárius eloszlást:

s=1/sum(v_1)*v_1
pretty_print(LatexExpr("\\mathbf{s}="),n(s,digits=4))

Szörfözzünk!

k=100
pretty_print(LatexExpr("P^{%.0f}="%(k)),n(P^k,digits=4))

Módosítsuk kicsit a játékszabályt: $p=0.1$ valószínűséggel beírunk egy véletlenszerűen választott címet, és $1-p=0.9$ valószínűséggel találomra kattintunk egy linkekre. Hosszú távon az időnk mekkora hányadát töltjük az egyes oldalakon?

Írjuk fel az átmenet-valószínűségek mátrixát:

p=1/10
J = matrix(QQ, [[1,1,1,1,1], [1,1,1,1,1], [1,1,1,1,1],[1,1,1,1,1],[1,1,1,1,1]])
PP = p/5*J + (1-p)*P
pretty_print(LatexExpr("P'="),n(PP,digits=4))

Határozzuk meg a $\lambda=1$ sajátértékhez tartozó sajátalteret:

pretty_print(LatexExpr("(P'-E)^T ="),n((PP-E).transpose(),digits=2),LatexExpr("\\rightsquigarrow"),n((PP-E).transpose().rref(),digits=4))

A sajátaltér egydimenziós, egy bázisvektora például:

vv_1 = (PP-E).transpose().rref().columns()[-1]*(-1)+vector([0,0,0,0,1])
pretty_print(LatexExpr("\\mathbf{v}'_1="),n(vv_1,digits=4));

Határozzuk meg a stacionárius eloszlást:

ss=1/sum(vv_1)*vv_1
pretty_print(LatexExpr("\\mathbf{s}'="),n(ss,digits=4))

Szörfözzünk!

k=100
pretty_print(LatexExpr("P'^{%.0f}="%(k)),n(PP^k,digits=4))

Bővebben lásd: The $25,000,000,000 Eigenvector: The Linear Algebra behind Google.