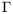 be a
discrete subgroup of the group of affine transformations
be a
discrete subgroup of the group of affine transformations 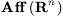 which acts discretely and properly discontinuously on
which acts discretely and properly discontinuously on 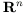 .
(Recall that
.
(Recall that 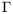 acts discretely
and properly discontinuously if for any compact
acts discretely
and properly discontinuously if for any compact 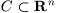 the set of
the set of 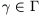 with
with 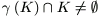 is
finite.)
is
finite.)Conjecture. (L. Auslander,1964)
If
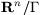 is compact, then
is compact, then 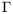 is virtually solvable, that is it admits a solvable subgroup with
finite index.
is virtually solvable, that is it admits a solvable subgroup with
finite index.Auslander's conjecture plays a central role in the study of compact space forms on symmetric spaces. It was studied by several distinguished authors, including L. Auslander, J. Milnor, G. A. Margulis, S. Friedland, Y. Kamishima, T. Kobayashi, G. Tomanov, etc. The continuous version of Auslander's conjecture was proved by T. Kobayashi.
My method is to extend Radon transform to the space of bounded distributions and reduce the non existence of non commutative free subgroup in
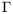 to summability conditions for the Radon transform of an appropriately
chosen
bounded distribution.
to summability conditions for the Radon transform of an appropriately
chosen
bounded distribution.