Algebrai görbének nevezzük egy kétváltozós f(X,Y) polinom zéróhelyeinek halmazát. Másodfokú polinom esetében ez kúpszeletet jelent, amelyeknek a beható vizsgálata már a középiskolában elkezdődik. Harmadfokú polinomok esetén azonban számos érdekes új jelenséggel találkozunk, amint azt az alábbi példák is mutatják.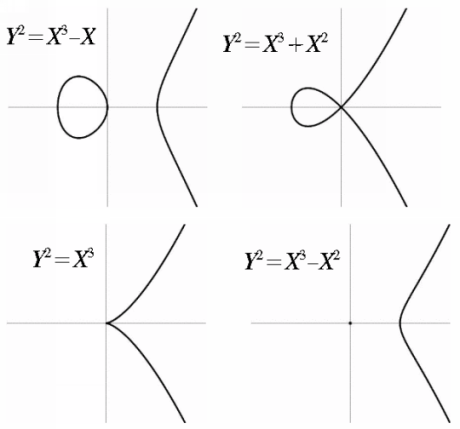

Az első esetben a görbe minden pontjában sima, de szétesik két komponensre. A többi háromnál az origóban valami szabálytalanság történik, és ezek mind különböző típusúak: a másodiknál rendesen átmetszi magát a görbe, a harmadiknál csak megtörik, a negyediknél egy izolált ponttal rendelkezik.

Az előadáson részletesen tárgyalni fogjuk az ilyen szabálytalanságokat. Beszélünk továbbá két görbe metszésének tulajdonságairól is, különös hangsúllyal a harmadfokú görbékre. Egy n-edfokú és egy m-edfokú polinom görbéjének metszéspontjainak a száma összefügg azzal a középiskolában is feltehető kérdéssel, hogy egy kétismeretlenes, két magasabbfokú egyenletből álló egyenletrendszernek hány megoldása van.