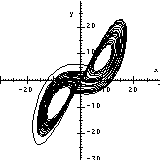
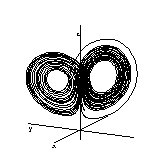
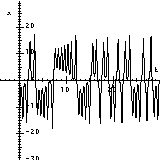
Lorenz's equation is one of the most tipical examples considered in the theory of ordinary differential equations. The first picture is the usual way of displaying the solutions: a projection to the (x,y) plane. The second picture is a 3 dimensional graphics of the solution. The third picture shows the x component of the solution as a function of t.
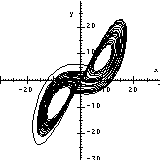
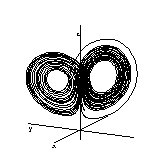

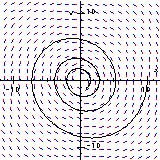
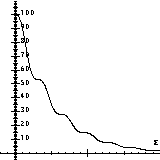
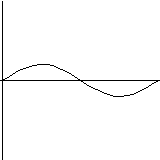
Another usual example is the damped pendulum. You can draw up the phase space with the direction field and the solution (first picture) and the energy function E=x*x+v*v (second picture). At the same time you can print out numerical values of t, x, v and E.
t x v E
0.04000 9.99200 -0.39840 99.99879
0.08000 9.96813 -0.79299 99.99253
0.12000 9.92857 -1.18317 99.97632
0.16000 9.87349 -1.56835 99.94545
0.20000 9.80311 -1.94795 99.89540
0.24000 9.71766 -2.32143 99.82188
0.28000 9.61740 -2.68823 99.72088
0.32000 9.50260 -3.04781 99.58864
0.36000 9.37358 -3.39967 99.42172
0.40000 9.23063 -3.74331 99.21698
0.44000 9.07412 -4.07824 98.97160
0.48000 8.90438 -4.40399 98.68313
0.52000 8.72180 -4.72013 98.34943
0.56000 8.52677 -5.02622 97.96875
0.60000 8.31971 -5.32186 97.53969
0.64000 8.10103 -5.60665 97.06121
0.68000 7.87118 -5.88024 96.53266
0.72000 7.63061 -6.14227 95.95371
0.76000 7.37980 -6.39241 95.32444
0.80000 7.11922 -6.63038 94.64526
0.84000 6.84938 -6.85587 93.91692
0.88000 6.57076 -7.06864 93.14051
0.92000 6.28389 -7.26844 92.31745
0.96000 5.98928 -7.45506 91.44945
1.00000 5.68748 -7.62831 90.53854
1.04000 5.37902 -7.78801 89.58700
1.08000 5.06444 -7.93403 88.59737
1.12000 4.74430 -8.06623 87.57244
1.16000 4.41915 -8.18452 86.51518
1.20000 4.08954 -8.28881 85.42878
1.24000 3.75604 -8.37906 84.31658
1.28000 3.41922 -8.45524 83.18208
1.32000 3.07962 -8.51732 82.02889
1.36000 2.73783 -8.56534 80.86070
1.40000 2.39440 -8.59931 79.68128
1.44000 2.04988 -8.61930 78.49444
1.48000 1.70485 -8.62540 77.30401
1.52000 1.35985 -8.61769 76.11381
1.56000 1.01544 -8.59631 74.92762
1.60000 0.67215 -8.56139 73.74919
1.64000 0.33052 -8.51310 72.58216
1.68000 -0.00890 -8.45163 71.43009
1.72000 -0.34561 -8.37717 70.29641
1.76000 -0.67908 -8.28995 69.18441
1.80000 -1.00881 -8.19021 68.09721
1.84000 -1.33430 -8.07821 67.03776
1.88000 -1.65507 -7.95422 66.00882
1.92000 -1.97064 -7.81854 65.01294
1.96000 -2.28055 -7.67147 64.05243
2.00000 -2.58436 -7.51335 63.12939
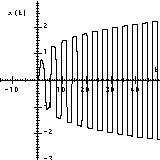
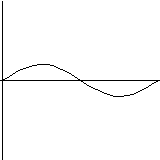
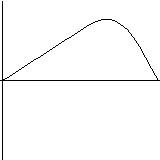
A functional differential equation can be solved and drawn just as easily. For example, the solution of the equation x'(t):=-a(t)*h(x(t))*x(t)-g(t,x(t-r(t))) (a, h, g and r are user defined functions) is shown on the next picture:
So far DifEqu has two kind of partial differential equations built in: PDE's on the line or PDE's on the plane. Mathematically it means that the unknown function depends on t and x or t, x and y, respectively. PDE's with more than two variables can also be programmed in DifEqu, I just did not have the time. Let us see the string with non-zero boundary conditions and the membrane with zero boundary conditions:
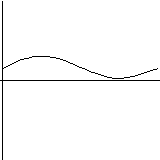
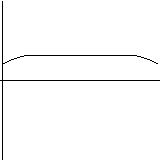
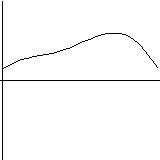
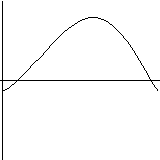
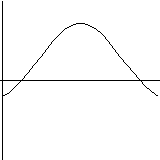
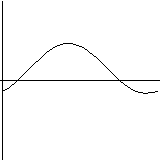




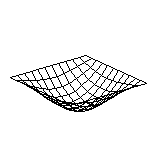
Of course, all of the above are just examples of the use of DifEqu, one can solve other equations, display it a different way or can write a program for solving an entirely different problem.
If this program seems to be suitable for your research, download this program to find it out.