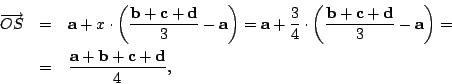|
A tetraéder súlypontja
Induljunk ki a Descartes-féle 3 dimenziós derékszögű koordináta-rendszerből!
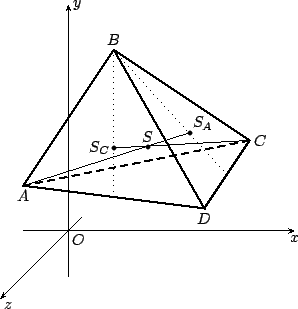
Vegyünk egy szabályos tetraédert, melynek csúcsai legyenek 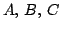 és
és 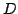 , a koordináta-rendszer origóját jeöljük , a koordináta-rendszer origóját jeöljük 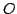 -val, s az -val, s az
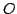 -ból a csúcsokba mutató vektorokat jelöljük rendre -ból a csúcsokba mutató vektorokat jelöljük rendre
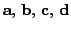 vektorokkal.
vektorokkal.
Tudjuk, hogy a tetraéder lapjait alkotó háromszögek
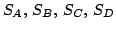 súlypontjaiba mutató vektorok rendre
súlypontjaiba mutató vektorok rendre
A tetraéder súlypontját az
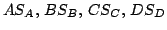 szakaszok metszéspontjaként definiáljuk, meggondolható, hogy ezeknek
a szakaszoknak valóban van metszéspontjuk, mégpedig egyetlen egy.
Jelöljük ezt a pontot
szakaszok metszéspontjaként definiáljuk, meggondolható, hogy ezeknek
a szakaszoknak valóban van metszéspontjuk, mégpedig egyetlen egy.
Jelöljük ezt a pontot 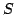 -sel. -sel.
Mivel 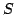 illeszkedik az illeszkedik az 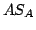 szakaszra, előállítható szakaszra, előállítható
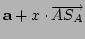 alakban, ahol
alakban, ahol 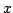 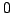 és és 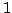 közötti valós szám. Hasonlóan, közötti valós szám. Hasonlóan, 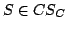 miatt előállítható
miatt előállítható
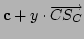 alakban
is ( alakban
is (![$y\in[0,1]$](img17.png) ). De ). De
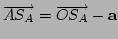 és
és
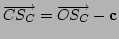 ,
vagyis a fentiek alapján az ,
vagyis a fentiek alapján az
és az
egyenletekhez jutunk. A jobb oldalakat egyenlővé téve az
egyenlőség adódik, amelyben minden egyes vektort egy oldalra rendezve
az
összefüggést kapjuk. Ez
alakba is írható. Az 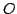 pont, továbbá az pont, továbbá az 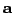 , ,
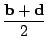 és
és 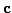 vektorok általános helyzetben nem esnek egy síkba,
mivel a középső vektor éppen a vektorok általános helyzetben nem esnek egy síkba,
mivel a középső vektor éppen a 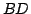 oldal felezőpontja (nagyon speciális
esetben előfordulhat, hogy egy síkba esnek). Emiatt általában ezen
három vektor lineáris kombinációja (vagy másképpen: súlyozott
összege) csak úgy lehet a nullvektor, ha a súlyok mindegyike 0. Ebből
pedig az adódik, hogy -- mivel oldal felezőpontja (nagyon speciális
esetben előfordulhat, hogy egy síkba esnek). Emiatt általában ezen
három vektor lineáris kombinációja (vagy másképpen: súlyozott
összege) csak úgy lehet a nullvektor, ha a súlyok mindegyike 0. Ebből
pedig az adódik, hogy -- mivel
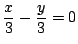 --
-- 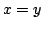 , továbbá -- például , továbbá -- például
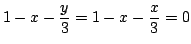 miatt
miatt
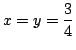 . Ebből világosan látszik,
hogy az . Ebből világosan látszik,
hogy az 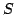 pont éppen negyedeli a tetraéder súlyvonalait. pont éppen negyedeli a tetraéder súlyvonalait.
A fentiek alapján most már az is látszik, hogy
azaz a tetraéder súlypontjába mutató vektor éppen a csúcsokba mutató
vektorok átlaga. (Vegyük észre, hogy sehol sem használtuk ki a tetraéder
szabályos voltát, tehát eredményünk általánosnak is tekinthető, tetszőleges
tetraéderre. A képlet pedig abban az esetben is ,,működik'', ha
az 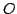 , illetve az , illetve az 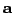 , ,
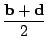 és
és  vektorok egy síkba esnének.) Ha a kapott eredményt
összevetjük a két pont (szakasz) illetve három pont (háromszög) súlypontjára
kapott képletekkel, könnyen általánosíthatunk: vektorok egy síkba esnének.) Ha a kapott eredményt
összevetjük a két pont (szakasz) illetve három pont (háromszög) súlypontjára
kapott képletekkel, könnyen általánosíthatunk:
Tetszőleges homogén poliéder súlypontját meghatározhatjuk úgy,
hogy a csúcsokba mutató vektoroknak a számtani közepét vesszük.
| |
![]() súlypontjaiba mutató vektorok rendre
súlypontjaiba mutató vektorok rendre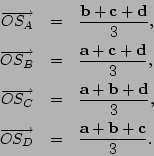
![]() illeszkedik az
illeszkedik az ![]() szakaszra, előállítható
szakaszra, előállítható
![]() alakban, ahol
alakban, ahol ![]()
![]() és
és ![]() közötti valós szám. Hasonlóan,
közötti valós szám. Hasonlóan, ![]() miatt előállítható
miatt előállítható
![]() alakban
is (
alakban
is (![]() ). De
). De
![]() és
és
![]() ,
vagyis a fentiek alapján az
,
vagyis a fentiek alapján az
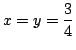 . Ebből világosan látszik,
hogy az
. Ebből világosan látszik,
hogy az