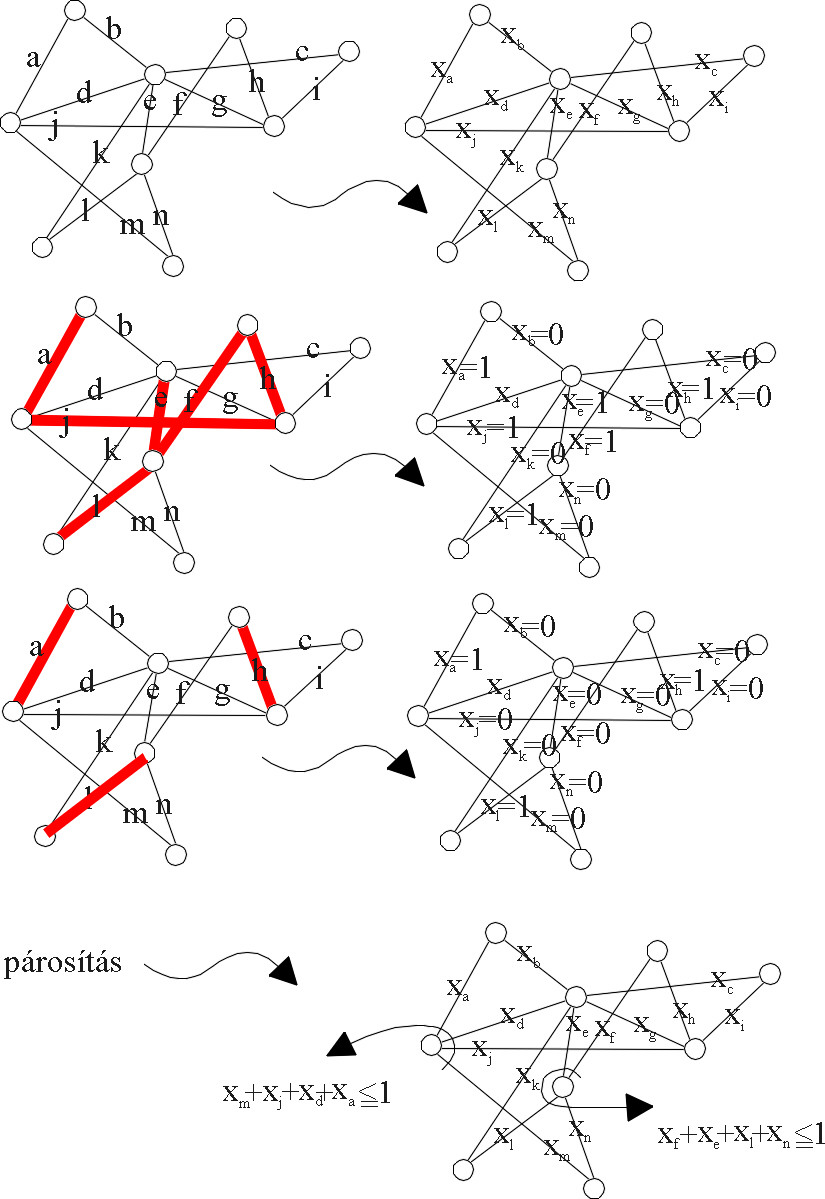
Adott egy G páros gráf. Mi a legnagyobb párosításának mérete? Ezt a problémára adunk egy újmegközelítést.
Minden e élre vezessünk be egy új változót (egy új betűt) xe-t. Ezen változóknak 0-1 értékeket adva kódolhatunk egy kiválasztott élhalmazt. kiválasztott e élre xe=1, míg e ki nem választása esetén xe=0. Egy kiválasztott élhalmaz akkor és csak akkor lesz párosítás, ha egyik csúcsnál sem fut össze kettő vagy több kiválasztott él. Ez algebrai módon is megfogalmazható. Az egy csúcsban összefügő élekhez rendelt változók összege nem haladja meg 1-et. Az összes csúcsra felírva ezt lineáris egyenlőtlenségek egy rendszerét kapjuk, amelynek 0-1 megoldásai pontosan a párosításokat kódoló értékelések. Ha ezen feltétel mellett a változók összegét (ami a kódolt élhalmaz elemszáma) maximálizáljuk, akkor a fenti párosítási problémát oldjuk meg.
Példa:

Az algebraizált változat az egész értékű programozás (IP) egy speciális esete. Megoldására az egész értékű programozás áltlánosmódszerei alkalamzhatók (például Gomory-vágások módszere). Az IP algoritmusok azonban nagyon áltlánosak és lassúak. Páros inputok esetén egyszerűbb mód is van a kezelésre.
A fenti IP feladat lineáris programozási (LP) relaxációja, ha az xe értéke {0,1}-beli helyettesítjük az 0<=xe<=1 feltételekkel. Ezzel persze a megengedett megoldások kombinatorikus értelmezése megszűnik.
Példa: Legyen G a C5 gráf, azaz az öthosszú kör. Az öt élhez rendelt változók legyenek x, y, z, v, w (sorrendjük a körmenti sorrend). Az egy csúcsban összefutó élpárokra a hozzárendelt változók összege legfeljebb 1: x+y<=1, y+z<=1, z+v<=1, v+w<=1, w+x<=1. A 0<=x, y, z, v, w <=1 feltétel mellett x=y=z=v=w=1/2 egy megengedett megoldás, aminél a változók összege 5/2, meghaladja 2-t a legnagyobb párosítás mértét, az x, y, z, v, w változókra 0-1 feltételt téve kapott IP feladat optimális megoldása.
A következő tétel azt mondja meg, hogy páros gráfok esetén az LP relaxáció bázismegoldásai automatikusan egészek lesznek. Azaz az LP feladat megoldása (szimplex módszerrel, vagy valamelyik belső pontos módszer, mondjuk Karmakar módszerrel) az optimum értékeként megadja a legnagyobb párosítás méretét.
Lemma: Legyen M egy G páros gráf pont-él illeszkedési mátrixa. ekkor M minden négyzetes almátrixának determinánsának értéke -1, 0 vagy 1.
Bizonyítás: A négyzetes almátrix méretére vonatkozó indukcióval bizonyítunk. 1×1-es almátrix determinánsa az almátrix egyetlen eleme, ami M esetén 0 vagy 1. Tegyük fel, hogy k-nál kevesebb sort (és így oszlopot is ) tartalmazó négyzetes almátrixokra tudjuk az állítást. Legyen A egy k×k méretű almátrix. Ha A-nak van csupa 0-t tartalmazó oszlopa, akkor készen vagyunk,mert determinánsa 0. Ha A-nak van egy darab 1-est és további 0-kat tartalmazó oszlopa, akkor ezen oszlop szerint kifejtve deteminánsát és hivatkozva az indukciós feltevésre készen vagyunk. Mivel M minden oszlopában pontosan két darab 1-es és további 0-k vannak ezért az egyetlen nem tárgyalt eset, az amikor A minden oszlopában két darab 1-es és további 0-k szerepelnek. M sorai G csúcsaival vannak azonosítva. G páros mivolta miatt G csúcsai két színosztályba sorolhatók (mondjuk piros és kék). Ennek megfelelően M sorai is lehetnek piros, illetve kék sorok. M minden oszlopában lévő két 1-es közül az egyik piros, a másik kék sorba esik. Ez igaz lesz az A részmátrixra is. Így A piros oszlopait összeadva a csupa 1-es vektort kapjuk. Ugyanerre az eredményre jutunk, ha A kék sorait adjuk össze. Ez a felismerés A sorai között egy nem triviális lineáris összefüggés, ami miatt determinansa 0, azaz újbó készen vagyunk ( most ismét az indukcióra való hivatkozás nélkül.
Következmény: A párosítási feladat IP problémaként való megfogalmazásának LP relaxációjának bázismegoldásai automatikusan egészek lesznek. Azaz az LP feladat megoldása (szimplex módszerrel, vagy valamelyik belső pontos módszer, mondjuk Karmakar módszerrel) az optimum értékeként megadja a legnagyobb párosítás méretét.
Bizonyítás: A következmény LP feladatát oldjuk meg szimplex módszerral. Ezen megoldás alatt kezelt mátrixnak lényeges része a lemmában szereplő pont-él illeszkédési mátrix. A szimplex algoritmus outputja egy bázis megoldás, ami Kramer-szabály alapján két determináns hányadosa. A determinánsok mátrixai egész eleműek és a nevezőben szereplő determináns -1 vagy 1. Így az output is egész értékű.
Megjegyzés: A fenti gondolatmenetben a célfüggvény együtthatói nem játszottaks zerepet. Ha a változók összege helyett a változók egy lineáris függvényét vizsgáljuk akkor is alakalmazható lineáris programozási megközelítésünk. A célfüggvény ezen módosítása a súlyozott párosítási probléma.