Ez utóbbi állítás igazolása: Vegyünk egy tetszõleges algoritmust és futassuk az algoritmust addig, míg a szomszédsági mátrix egyik elemét elolvassa. Ott egy 0-t vagy egy 1-et talál. Ettõl függõen az algoritmus esetleg különbözõképpen fut tovább, amíg egy újabb bitet el nem olvas és ekkor a futás további részét két további alesetre szakíthatjuk szét... Az algoritmus ezen struktúráját ``lerajzolva '' jutunk el a döntési fa fogalmához.
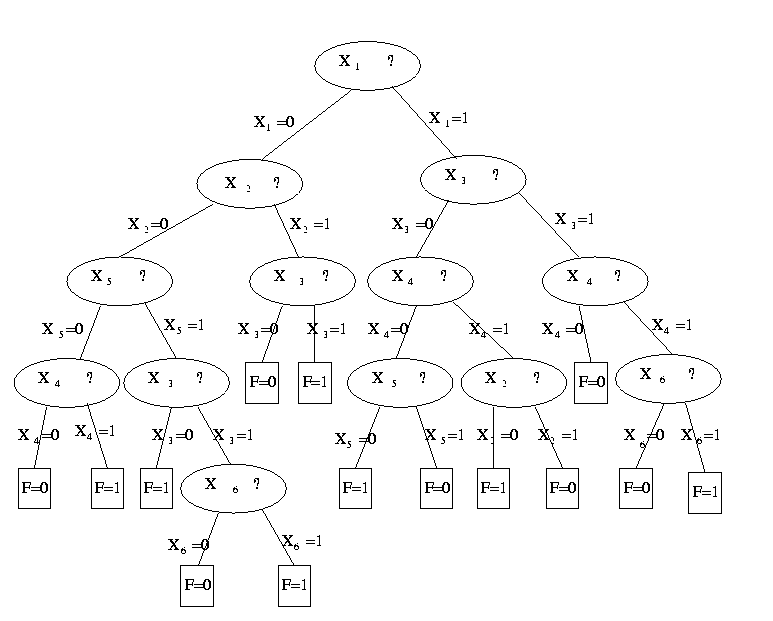
Az alábbi ábra egy példát mutat döntési fára.

Egy jó algoritmus esetén a döntési fa minden számítási ágán összegyûlik annyi információ, hogy a megoldandó probléma eldöntéséhez elég legyen.
Azt fogjuk igazolni, hogy minden helyes döntési fa mélysége n(n-1)/2.
Ehhez egy játékot vizsgálunk: Egy kérdezõ és egy válaszoló lesz a két játékos. A kérdezõ az ismeretlen illeszkedési mátrix egy-egy elemére kérdez rá és a válaszoló megmondja, hogy a kérdezett elem 0 vagy 1. A kérdezõ addig kérdez, amíg el nem tudja dönteni (az összegyûjtött információk alapján), hogy az ismeretlen gráfban van-e izolált pont. Belátjuk, hogy a válaszolónak van olyan stratégiája, hogy a kérdézõt n(n-1)/2 kérdésre kényszerítse.
A stratégia legyen a következõ:
Ezekután nézzük meg az állításunk igazolását:
X(t) a kérdezõ-válaszoló protokol futásának t-edik idõpillanatában azon csúcsok halmaza, amelyekre illeszkedik él a kérdezõ eddig kapott válaszai alapján. Az ismertetett válaszoló stratégia olyan, hogy X(t)-n belül nincs megkérdezetlen él.
Mindenekelõtt vizsgáljuk meg az X függvény néhány tulajdonságát. A kérdés megkezdése elótt az X halmaz értéke természetesen az üreshalmaz. Az elsõ kérdés (legyen ez ``u és v összekötött?'') után az X halmaz értéke az u és v csúcskat tartalmazó halmaz (X(1)={u,v}). Az X függvény természetesen monoton, azaz t < s esetén X(t) részhalmaza (nem feltétlenül valódi részhalmaza) X(s)-nek.
Belátjuk, hogy amikor a kérdezõ tudja, hogy G-ben van-e izolált csúcs, akkor mindent megkérdezett, sõt az adódik, hogy az algoritmus végén az X halmaz a teljes csúcshalmaz.
Ez ellentmond a válaszoló strtégiájának. Vizsgáljuk meg, hogy hogyan változik az az Y(t) halmaz, amely azon csúcsokat tartalmazza, amelyek és v által tartalmazott párokat a kérdezõ megkérdezte (és feltételezésünk szerint 0, azaz ``nem összekötött'' választ kapott). Y(0) az üres halmaz. Feltételezésünk szerint az algoritmus végén az Y halmaz a V(G)-{v} halmaz. Y(t+1) vagy azonos Y(t)-vel vagy egyetlen egy csúccsal történõ bõvítése Y(t)-nek. (Azt is mondhatjuk, hogy a folytonossági és monoton tulajdonság egy diszkrét változatát teljesi;ti az Y függvény.) Az algoritmus végen az Y halmaz ``utoléri '' az X=(X-{v}) halmazt. Lesz a kérdezés folyamán az utolsó olyan idõpillanat (legnagyobb t érték) amikor Y(t) nem tartalmazza X(t) halmazt. t választása miatt Y(t+1) tartalmazza X(t)-t. t-rõl t+1-re ugorva (feltéve a t+1-edik kérdést) az Y halmaz legfeljebb egy elemmel nõ (nõni is fog, hiszen utol kell érnie a nem csökkenõ X halmazt). Ez csak úgy lehet, ha X(t+1) és Y(t+1) egyenlõ. Továbbá X(t+1)=X(t) hiszen Y növekedéséhez szükségszerû, hogy az utolsó kérdés egy v-t tartalmazó pár legyen, amely kérdésre feltételezésünk szerint 0 választ kell kapnunk, azaz az X halmaz nem változik.
Y(t)-hez képest Y(t+1) nõ, azaz a t+1-edik kérdés egy v-t tartalmazó pár volt: {v,v'} (Y(t+1)=Y(t)U{v'}). Mit csinál a válaszadó? A leírt stratégia alapján megnézi, hogy mi történne, ha ``összekötött''-et válaszolna (X(t+1)=X(t)U{v,v'}=X(t)U{v}). Ekkor meg kell vizsgálnia, hogy ezen halmazon belül minden csúcspár tesztelt-e. X(t)-n belül mindennek teszteltnek kell lenni. v és X(t) elemei által alkotott párok viszont Y(t+1)=X(t+1)=X(t) és az T halmaz definíciója miatt már teszteltek. A startégiánk viszont ekkor azt mondja, hogy a válaszoló 1-gyel váalszoljon. Ez ellentmond feltevésünknek.