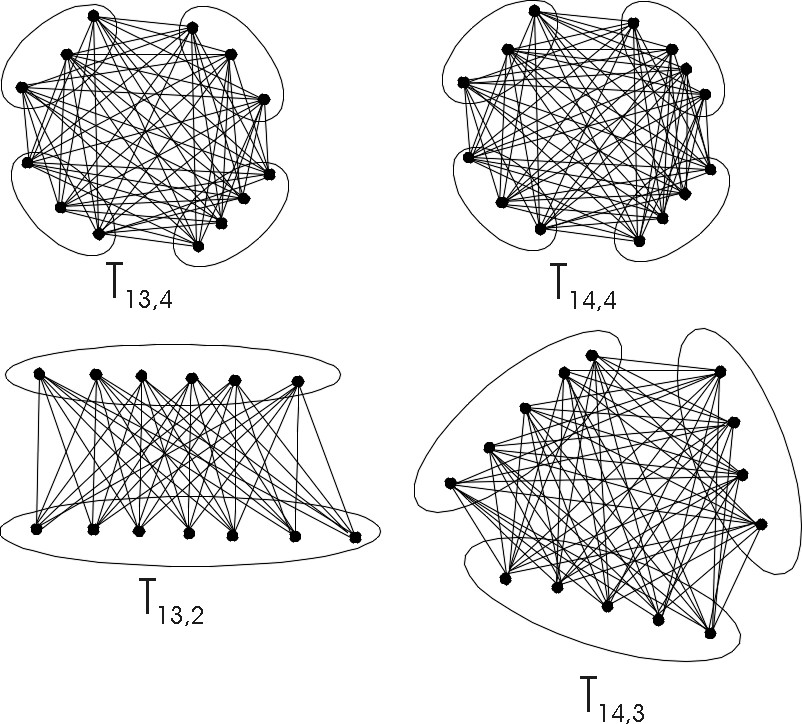
Definíció: Az n pontú, k részes Turán-gráfot Tn,k-t úgy kapjuk, hogy az n elemű V csúcshalmazt k darab majdnem egyenlő részre osztjuk (azaz az egyes részek/osztályok elemszáma maximum 1-gyel különbözzön) és a különböző osztályok között az összes élt behúzzuk, míg az egyes osztályokon belül nincs él.
Megjegyzés: A fent definiált Tn,k egy izomorfia erejéig egyértelműen meghatározott gráf. A majdnem egyenlő részekre bontásoknál az előforduló osztály méreteknek n/k fel, illetve lekerekített értekei (n/k egész esetén ez egy lehetőség, n/k nem egész esetén ez kettő lehetőség az osztályméretre) közül kell kikerülni. Továbbá az egyes osztályméretekhez tartozó osztályok száma/multiplicitása is meghatározott.

A fontos észrevétel, hogy a Tn,k Turán-gráfban nincs k+1 elemű klikk. Valóban tetszőlegesen kivéve V-ből k+1 pontot a skatulya-elv szerint lesz két csúcs, amley a Turán-gráf deiníciójában szerepló osztályozás ugyanazon osztályából kerül ki, így nincsenek összekötve, így kivett pont k+1-esünk nem klikk.
Tétel: (Turán-tétel)
Ha G egy n pontú egyszerű gráf és
|E(G)|>|E(Tn,k)|, akkor G tartalmaz k+1 elemű klikket.
Megjegyzés: ha k<=n, akkor |E(Tn,k)| egy n pontú teljes gráf és a tétel nyilvánvalóan igaz (feltétele nem teljesülhet).
A tétel természetesen megfogalmazható a klikkek és független halmazok között kapcsolat kihasználásával.
Tétel: (Turán-tétel, komplementáris forma)
Legyen k< n.
Ha G egy n pontú egyszerű gráf és
|E(G)|< |E(T—n,k)|, akkor G tartalmaz k+1 elemű
független ponthalmazt.
A fenti állítást egy erősebb formában bizonyítjuk:
Tétel: (Turán-tétel, komplementáris erős forma)
Ha G egy n pontú egyszerű gráf és
|E(G)|<|E(T—n,k)|, akkor módosított
mohó algoritmus legalább k+1 elemű
független ponthalmazt talál.
Bizonyítás: Emlékeztetőnek idézzük fel a módosított mohó algoritmus analízisének melléktermékeként kapott lemmát:
Lemma: Ha G-n futtatva a módosított mohó algoritmust t elemű független halmazhoz jutunk, akkor |V(G)|-t felírhatjuk t darab ei pozitív egész összegeként úgy, hogy a (ei2) számok összege legfeljebb |E(G)| legyen. Ez a lemma másképpen is megfogalmazható. Ehhez vezessünk be egy fogalmat.
Definíció: Egy egyszerű gráfot ekvivalencia gráfnak nevezzük, ha komponensei teljes gráfok. Ha s komponense van, akkor s komponensű ekvivalencia gráfnak hívjuk.
Megjegyzés: A T—n,k komplementáris Turán-gráfok ekvivalencia gráfok, amely komponens száma megegyezik k-val a Turán-gráf osztályszámával.
Lássuk a korábbi lemma számunkra hasznos megfogalmazását.
Lemma ': Ha G-n futtatva a módosított mohó algoritmust t elemű független halmazhoz jutunk, akkor létezik egy t komponensű O ekvivalencia gráf, amelyre |V(O)|=|V(G)| és |E(O)|<= |E(G)|.
Turán-tétel komplementáris erős formáját indirekten bizonyítjuk: Tegyük fel, hogy G-ben a módosított mohó algoritmus legfeljebb k elemű független ponthalmazt talál. Ekkor G élszámát nem múlja felül egy legfeljebb k komponensű ekvivalencia gráf élszáma.
A tétel következik a következő lemmából.
Lemma: Az n pontú, legfeljebb k komponensű ekvivalencia gráfok között T—n,k a legkevesebb élszámú.
Az utolsó két lemma adja, hogy egy olyan gráf, amely esetén a módosított mohó algoritmus nem talál k+1 elemű független ponthalmaz élszáma legalább |E(T—n,k)|.
Lemma bizonyítása: A lemma véges sok ekvivalencia gráfot érint. Ezek közül a k-nál kevesebb komponensűek élszáma csökkenthető, ha az egyik komponens ponthalmazát kettéosztjuk. Így a minimális élhalmazú gráfot a k részesek között kell keresni. Ezek között a T—n,k-től különbözőek olyanok, hogy van két komponensük, amelyek pontszámának különbsége lgalább 2. Vegyünk egy ilyen O gráfot és legyen O ' az az ekvivalencia gráf, amelyet úgy kapunk, hogy O legnagyobb komponenséből (legyen ez M pontú) egy csúcsot átteszünk a legkisebb komponensébe (legyen ez m pontú). M-m>=2. Ekkor |E(O ')|=E(O)|-(M2)-(m2) +(M-12)+(m-12). Egyszerű számolás mutatja, hogy O élszámánál O ' élszáma kisebb. Így a vizsgált gráfok között csak T—n,k lehet a minimális élszámú.
Turán Pál a XX. századi magyar matematika egyik kiemelkedő alakja. Munkássága az analízis, számelmélet, gráfelmélet fejlődésére is nagy hatással volt. Életrajza az interneten magyar, angol és magyar nyelven is megtalálható.